Запись дифференциальных уравнений в символическом виде.

Будем рассматривать следующую систему

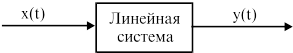
Рис.2.6

Пусть в общем случае линейная система описывается дифференциальным уравнением n-го порядка

... ... ,

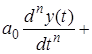
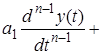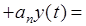
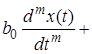
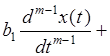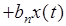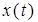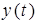где и соответственно входной и выходной сигналы системы. Преобразуем левую и правую части этого уравнения по Лапласу. В результате получим следующее дифференциальное уравнение в символическом виде

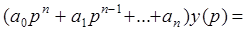
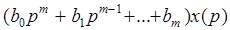, (2.11)

где 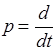- оператор дифференцирования.

Введем обозначения

= ,

= .

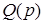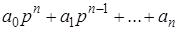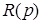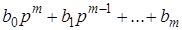Тогда уравнение (2.11) можно записать в более компактно

.

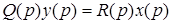Cтандартная форма записи линейных дифференциальных

Уравнений

Принято, что линейные дифференциальные уравнения не выше второго порядка записываются в стандартной форме, а именно:

- члены уравнения, содержащие выходную величину и ее производные, записываются в левой части уравнения;

- все остальные члены уравнения, записываются справа;

- коэффициент при выходной величине делают равным единице;

- коэффициенты при входных и выходных величинах и их производных являются либо постоянными времени, либо коэффициентами передачи (усиления).

Рассмотрим дифференциальное уравнение в символическом виде

.

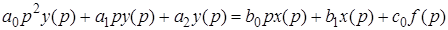Разделим обе части этого уравнения на 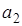и введем обозначения

, , , , .

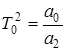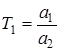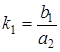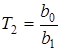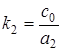Тогда

.

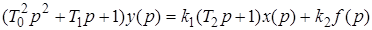Здесь 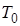, , 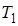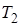- имеют размерность времени и называются постоянными времен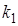и, и 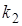- безразмерные коэффициенты передачи (усиления).