ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ
СВОЙСТВА
Преобразованием Лапласа называется следующее соотношение
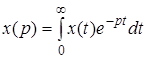 , (2.8)
, (2.8)
где 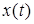 - функция вещественного переменного,
- функция вещественного переменного, 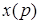 - функция комплексного переменного
- функция комплексного переменного 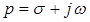 . Преобразование Лапласа ставит в соответствие функции действительного переменного
. Преобразование Лапласа ставит в соответствие функции действительного переменного 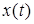 функцию комплексного переменного
функцию комплексного переменного 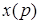 . Смысл преобразования Лапласа заключается в том, что оно переводит рассмотрение процесса, являющегося функцией действительного переменного, например времени, на комплексную плоскость с координатами
. Смысл преобразования Лапласа заключается в том, что оно переводит рассмотрение процесса, являющегося функцией действительного переменного, например времени, на комплексную плоскость с координатами 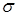 и
и 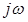 .
.
Функцию 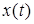 называют оригиналом, а функцию
называют оригиналом, а функцию 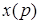 изображением по Лапласу или просто изображением. Преобразование Лапласа можно записать в символическом виде
изображением по Лапласу или просто изображением. Преобразование Лапласа можно записать в символическом виде
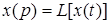 (2.9)
(2.9)
где 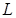 - оператор Лапласа.
- оператор Лапласа.
Функция 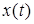 , являющаяся оригиналом, должна обладать следующими свойствами:
, являющаяся оригиналом, должна обладать следующими свойствами:
- должна быть определена и кусочно-дифференцируема на всей положительной числовой полуоси 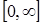 ;
;
- 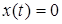 при
при 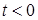 ;
;
- существуют такие положительные числа 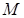 и
и 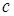 , что
, что 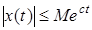 при
при 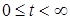 .
.
С помощью обратного преобразования Лапласа
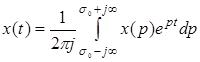 , (2.10)
, (2.10)
можно найти по известному изображению его оригинал. В нем интеграл берется вдоль любой прямой 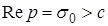 . Символически обратное преобразование Лапласа можно записать
. Символически обратное преобразование Лапласа можно записать
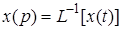 ,
,
где 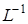 - обратный оператор Лапласа.
- обратный оператор Лапласа.
Рассмотрим основные свойства преобразования Лапласа.
1. Свойство линейности. Для любых постоянных 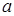 и
и 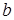
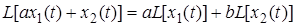 .
.
2. Дифференцирование оригинала.
Для первой производной
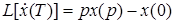 , где
, где 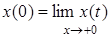 .
.
Для n-й производной
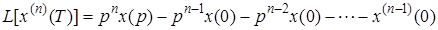 ,
,
где
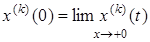 ,
, 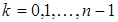 .
.
Если начальные условия нулевые
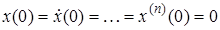 ,
,
то
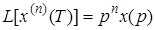 .
.
Таким образом, n-кратное дифференцирование оригинала при нулевых начальных условиях, соответствует умножению изображению на n-ю степень 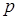 .
.
3. Интегрирование оригинала сводится к делению изображения на 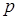 .
.
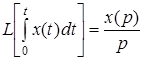 .
.
4. Теорема запаздывания. Для любого положительного 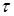
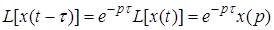 .
.
5. Теорема о свертке. Если 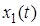 и
и 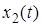 - оригиналы, а
- оригиналы, а 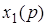 и
и 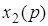 - их изображения, то
- их изображения, то
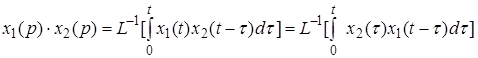 .
.
Интеграл правой части называется сверткой функций 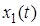 и
и 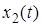 , который обозначают
, который обозначают 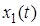 *
* 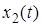
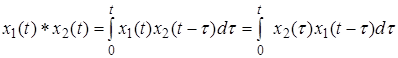 .
.
6. Теорема о предельных значениях. Если 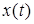 - оригинал, а
- оригинал, а 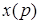 - его изображение, то
- его изображение, то
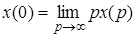 ,
,
и при существовании предела 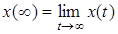 ,
,
справедливо записать
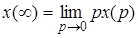 .
.
Дата добавления: 2019-12-09; просмотров: 1002;











