Передаточная функция звена имеет вид

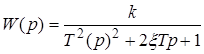 .
.
 Запишем АФЧХ звена
Запишем АФЧХ звена

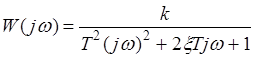 .
.
На Рис.4.7, 4.8 и 4.9 изображены соответственно переходные характеристики, АФЧХ и ЛЧХ колебательного звена при 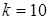 ,
, 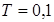 ,
, 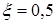 и
и 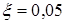 .
.
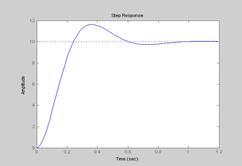
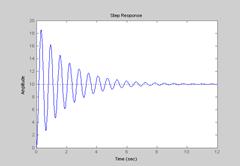
Рис.4.7.
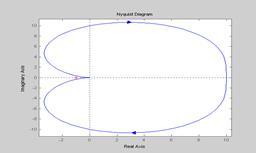
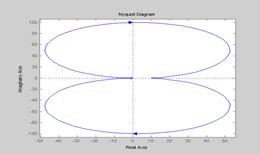
Рис.4.8.
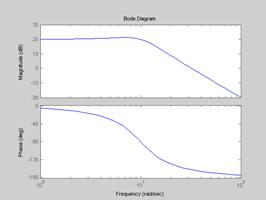
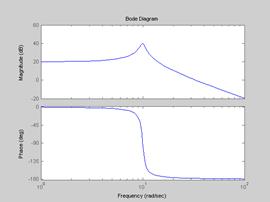
Рис.4.9.
Колебательным звеном описываются двигатели постоянного тока при некоторых значениях параметров, движение летательного аппарата относительно какой либо оси, поведение гироскопической системы и т. п.
Консервативное звено является частным случаем колебательного и описывает режим возникновения в той или иной системе незатухающих колебаний. На Рис.4.8 изображена переходная характеристика консервативного звена.
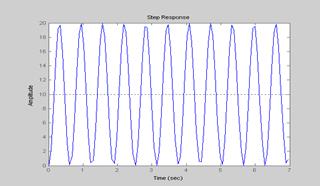
Рис.4.8.
Апериодическое звено второго порядка эквивалентно двум последовательно включенным апериодическим звеньям первого порядка.
Интегрирующее звено имеет следующее дифференциальное уравнение
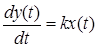 ,
,
где 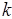 - коэффициент передачи (усиления) звена.
- коэффициент передачи (усиления) звена.
Его передаточная функция
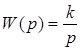 .
.
Частотные и переходная характеристики имеют вид
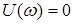 ,
, 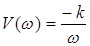 ,
,
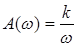 ,
, 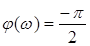 ,
, 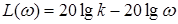 ,
,
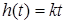 .
.
На Рис.4.9. и 4.10 представлены соответственно переходная характеристика и ЛЧХ звена
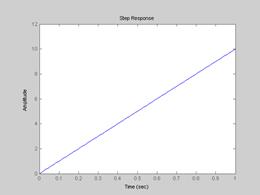
Рис.4.9.
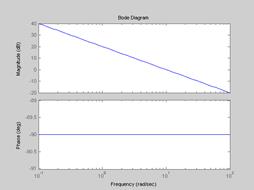
Рис.4.10.
Примером интегрирующего звена является электродвигатель, выходной величиной которого является угол поворота вала, являющейся интегралом от угловой скорости. К интегрирующему звену можно отнести гидравлический демпфер, причем входной является сила, приложенная к поршню, а выходной величиной будет являться перемещение штока.
Для дифференцирующего звена справедливо уравнение
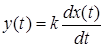 .
.
Дата добавления: 2019-12-09; просмотров: 771;











