ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ
|

Рис.2.4.
описывается следующим дифференциальным уравнением
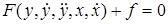 , (2.3)
, (2.3)
где 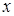 и
и 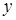 - соответственно входной и выходной сигналы,
- соответственно входной и выходной сигналы, 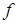 - возмущающее воздействие.
- возмущающее воздействие.
Уравнение (2.3) является нелинейным. Процесс исследования нелинейных систем существенно сложнее процесса исследования линейных. Поэтому исследование нелинейных систем стремятся свести к исследованию линейных. Процедура преобразования нелинейных уравнений в линейные называется линеаризацией.
Процедура линеаризации базируется на разложении нелинейных функций, входящих в уравнения, в ряд Тейлора. Необходимо отметить, что разложение какой либо функции в ряд Тейлора происходит в достаточно малых окрестностях некоторой точки. В качестве такой точки берется точка, соответствующая заданному режиму работы системы. В установившемся состоянии это может быть режим равновесия. Заметим, что отклонения реальных значений входных и выходных сигналов от их заданных значений в нормально работающей замкнутой автоматической системе не велико. Система работает по принципу парирования таких отклонений.
Обозначим переменные, соответствующие заданному режиму работы системы
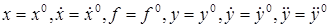 . (2.4)
. (2.4)
Введем отклонения реальных значений сигналов от требуемых
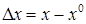 ,
, 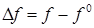 ,
, 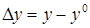 .
.
Тогда
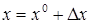 ,
, 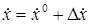 ,
, 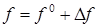 ,
, 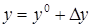 ,
, 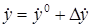 ,
, 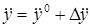 .
.
Рассматривая функцию 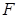 выражения (2.3) как функцию независимых переменных
выражения (2.3) как функцию независимых переменных 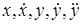 , разложим ее в ряд Тейлора в точке (2.4), соответствующей заданному режиму
, разложим ее в ряд Тейлора в точке (2.4), соответствующей заданному режиму
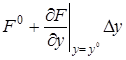 +
+ 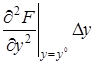 +
+ 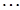 +
+ 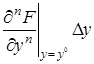 +
+
+ 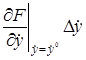 +
+ 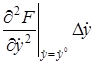 +
+ 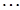 +
+ 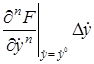 +
+
+ 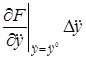 +
+ 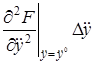 +
+ 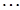 +
+ 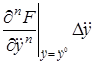 +
+
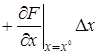 +
+ 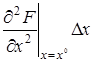 +
+ 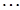 +
+ 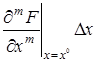 +
+
+ 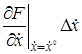 +
+ 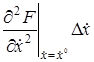 +
+ 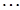 +
+ 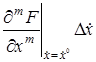 +
+ 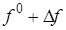 =0.
=0.
В этом выражении оставим только первые члены разложения, отбросив малые члены более высокого порядка.
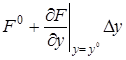 +
+ 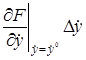 +
+ 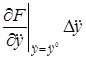 +
+
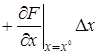 +
+ 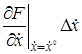 +
+ 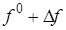 =0. (2.5)
=0. (2.5)
В заданном режиме уравнение (2.3) примет вид
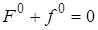 .
.
Вычтем это уравнение из (2.5), получим
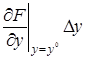 +
+ 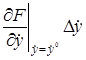 +
+ 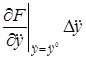
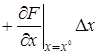 +
+ 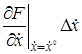
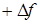 =0. (2.6)
=0. (2.6)
Введем обозначения
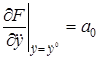 ,
, 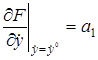 ,
, 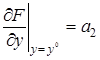 ,
, 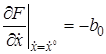 ,
, 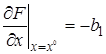 .
.
Подставив их в (2.6) и отбросив знак 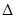 , получим линеаризованное уравнение в отклонениях
, получим линеаризованное уравнение в отклонениях
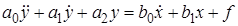 . (2.7)
. (2.7)
Линеаризация уравнения (2.3) была проведена в предположениях:
- отклонения входных 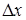 и
и 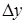 сигналов от их заданных значений малы,
сигналов от их заданных значений малы,
- функция 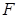 имеет непрерывные частные производные по всем своим аргументам в окрестности точки разложения, соответствующей заданному режиму,
имеет непрерывные частные производные по всем своим аргументам в окрестности точки разложения, соответствующей заданному режиму,
- линеаризованное уравнение (2.7) является уравнением в отклонениях.
|
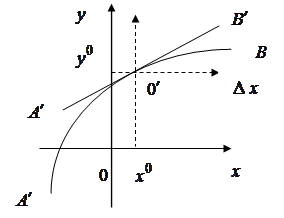 |
Рис.2.5.
В этом случае нелинейная зависимость между 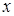 и
и 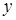 , выраженная
, выраженная
кривой 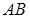 , в окрестностях точки разложения
, в окрестностях точки разложения 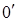 , заменена касательной
, заменена касательной 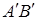 . Запись же уравнения в отклонениях, соответствует переносу начала координат в точку
. Запись же уравнения в отклонениях, соответствует переносу начала координат в точку 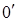 .
.
Дата добавления: 2019-12-09; просмотров: 839;











