Аналитический метод решения систем линейных однородных дифференциальных уравнений
Рассматривается система линейных однородных дифференциальных уравнений (СЛДУ) первого порядка
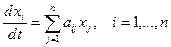 . .
| (7.14) |
Система (7.14), когда в левой части уравнений стоят производные, а правая часть производных не содержит, называется нормальной. Путем замены переменных (например, 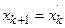 ) к нормальному виду может быть приведена любая нелинейная система ДУ с производными высших порядков.
) к нормальному виду может быть приведена любая нелинейная система ДУ с производными высших порядков.
В матричной форме записи система (7.14) может быть представлена уравнением:
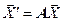 , ,
| (7.15) |
где
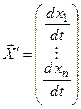 ;
; 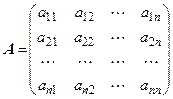 ;
; 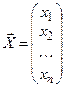 .
.
Пример. Привести к нормальной форме записи уравнение вида
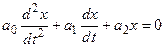 .
.
Выполним замену переменных 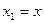 ,
, 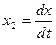 , тогда исходное ДУ преобразуется в систему
, тогда исходное ДУ преобразуется в систему
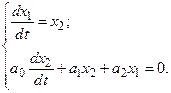
Эта система может быть представлена в виде, приемлемом для матричной формы
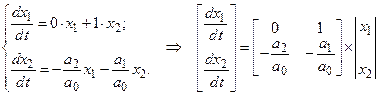
Принимая во внимание, что любая матрица является отражением линейного преобразования, можно заметить, что система ДУ ставит в соответствие вектору переменных вектор производных (образ исходного вектора), 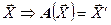 . Далее этот тезис будет расширен.
. Далее этот тезис будет расширен.
В разделе 7.5 было сказано, что существует такой базис (система собственных векторов 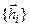 ), где матрица линейного преобразования является диагональной
), где матрица линейного преобразования является диагональной 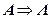 . В базисе
. В базисе 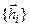
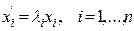 . Нетрудно получить решение представленных ДУ. Оно имеет вид
. Нетрудно получить решение представленных ДУ. Оно имеет вид
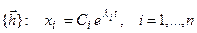 , ,
| (7.16) |
или в матричной форме
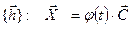 ,
,
где 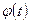 - функциональная матрица (квадратная, порядка n), диагональными элементами которой являются экспоненциальные функции
- функциональная матрица (квадратная, порядка n), диагональными элементами которой являются экспоненциальные функции 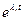 ,
, 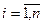 , а недиагональные элементы равны нулю.
, а недиагональные элементы равны нулю.
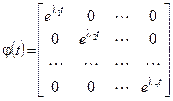 .
.
Учитывая преобразования перехода к старому базису, получаем
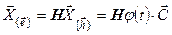 , ,
| (7.17) |
где Н - матрица, состоящая из собственных векторов 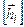 .
.
При t=0 матрица 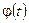 преобразуется в единичную, В результате получаем
преобразуется в единичную, В результате получаем
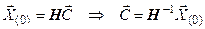 .
.
Окончательно, решение СЛДУ
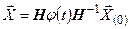
| (7.18) |
Пример. Найти решение системы линейных однородных дифференциальных уравнений
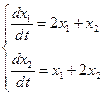
с начальными условиями 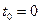 :
: 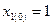 ,
, 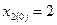 ,.
,.
Матрица А имеет вид: 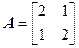 . Для нахождения собственных чисел составим характеристический определитель
. Для нахождения собственных чисел составим характеристический определитель
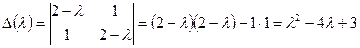 .
.
Найдем корни характеристического уравнения 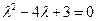 , которые одновременно являются собственными числами матрицы А:
, которые одновременно являются собственными числами матрицы А: 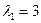 и
и 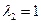 .
.
Определим собственные вектора.
Для 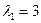 характеристическая матрица имеет вид
характеристическая матрица имеет вид
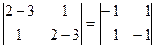 .
.
Строки полученной матрицы являются линейно-зависимыми. Решим систему уравнений для определения первого собственного вектора
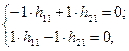
при 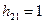 получим значение
получим значение 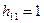 , тогда
, тогда 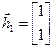 .
.
Аналогично определим второй собственный вектор 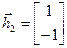 .
.
Матрица 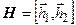 имеет вид
имеет вид 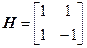 , а обратная к ней
, а обратная к ней
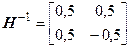 .
.
Решение рассматриваемой системы дифференциальных уравнений получается в виде (7.18),
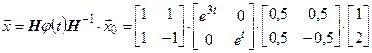
или 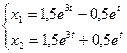 .
.
Дата добавления: 2020-07-18; просмотров: 842;











