Частотные характеристики
Частотные характеристики системы могут быть получены при рассмотрении реакции системы на гармонические воздействия разной частоты. При прохождении через линейную систему гармонического сигнала разной частоты у выходного сигнала в общем случае изменяются только амплитуда и фаза, частота остается неизменной. К частотным характеристикам относятся :
- амплитудно - фазовая частотная характеристика (АФЧХ),
- амплитудная частотная характеристика (АЧХ),
- фазовая частотная характеристика (ФЧХ),
- логарифмическая амплитудная частотная характеристика (ЛАЧХ),
- логарифмическая фазовая частотная характеристика (ЛФЧХ).
Рассмотрим частотную передаточную функцию , которая получается из передаточной функции (2.12) путем замены 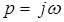 , где
, где 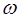 является частотой
является частотой
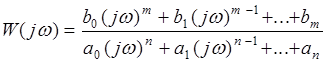 . (3.3)
. (3.3)
Функцию 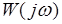 можно записать в следующем виде
можно записать в следующем виде
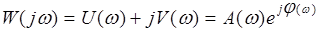 , (3.4)
, (3.4)
где
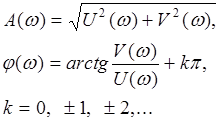
На комплексной плоскости 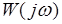 представляет собой вектор, при изменении частоты
представляет собой вектор, при изменении частоты 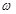 от
от  до +
до +  конец вектора
конец вектора 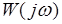 описывает кривую, называемую амплитудно - фазовой частотной характеристикой (АФЧХ). Например АФЧХ может иметь следующий вид
описывает кривую, называемую амплитудно - фазовой частотной характеристикой (АФЧХ). Например АФЧХ может иметь следующий вид
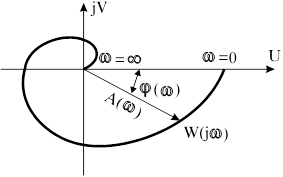
Рис.3.3.
Длина вектора 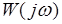 равна
равна 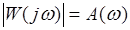 . График
. График 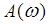 является амплитудной частотной характеристикой (АЧХ)
является амплитудной частотной характеристикой (АЧХ)
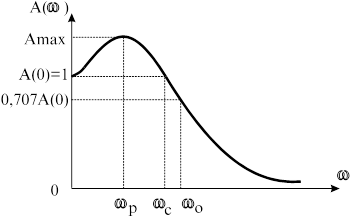
Рис.3.4.
На этой характеристике 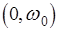 - полоса пропускания системы,
- полоса пропускания системы, 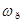 - резонансная частота, а
- резонансная частота, а 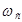 - частота среза.
- частота среза.
Аргумент 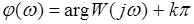 , представляющий собой угол между вектором
, представляющий собой угол между вектором 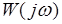 и действительной положительной полуосью называют фазовой частотной характеристикой (ФЧХ). Кроме того, в соответствии с (3.4) график действительной части
и действительной положительной полуосью называют фазовой частотной характеристикой (ФЧХ). Кроме того, в соответствии с (3.4) график действительной части 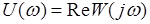 называется вещественной частотной характеристикой, а график мнимой части
называется вещественной частотной характеристикой, а график мнимой части 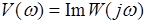 - мнимой частотной характеристикой.
- мнимой частотной характеристикой.
Наряду с перечисленными частотными характеристиками самое широкое применение находят логарифмические частотные характеристики (ЛЧХ), а именно логарифмические амплитудно-частотные и фазо-частотные характеристики - соответственно ЛАЧХ и ЛФЧХ. Для ЛАЧХ по оси ординат откладывают 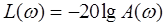 . Единицей измерения
. Единицей измерения 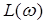 является децибел . Для ЛФЧХ по оси ординат откладывается значение угла в градусах . По оси абсцисс откладывают частоту
является децибел . Для ЛФЧХ по оси ординат откладывается значение угла в градусах . По оси абсцисс откладывают частоту 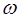 в логарифмическом масштабе, причем на отметке, соответствующей значению
в логарифмическом масштабе, причем на отметке, соответствующей значению 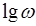 , записывается само значение частоты
, записывается само значение частоты 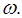
Ось ординат проходит не через точку 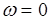 , так как в этом случае
, так как в этом случае 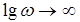 , а через произвольную точку обычно малой частоты.
, а через произвольную точку обычно малой частоты.
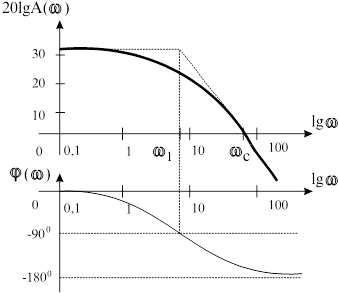
Рис. 3.5.
На рисунке 3.5 изображена так называемая реальная ЛАЧХ. На практике обычно ограничиваются построением асимптотических ЛАЧХ, представляющих собой ломаные линии (на рисунке пунктирная линия). Частоты при которых пересекаются асимптоты называются сопрягающими, они связаны с постоянными времени системы соотношением 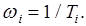
Дата добавления: 2019-12-09; просмотров: 929;











