УРАВНЕНИЯ ДИНАМИКИ И СТАТИКИ

Динамика рассматривает состояние движения, ход развития процессов во времени. Динамика процессов обычно описывается дифференциальными или разностными уравнениями.

Будем рассматривать систему

Рис.2.1.

Поведение исследуемой системы описывается дифференциальными уравнениями. Так зависимость выходного сигнала 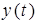от входного 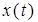в общем случае можно описать следующим дифференциальным уравнением

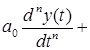
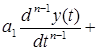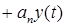
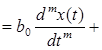
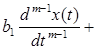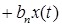... ... , (2.1)

где

, , , … , ,

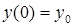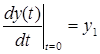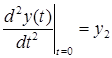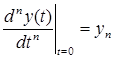- начальные условия. Уравнение 2.1. является уравнением динамики рассматриваемой системы.

Пусть поведение системы Рис.2.1 описывается уравнением

.

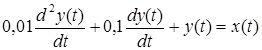Будем предполагать, что 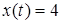. Входной сигнал 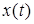и сигнал на выходе системы 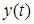, полученный в результате моделирования при нулевых начальных условиях, изображены на Рис.2.2.

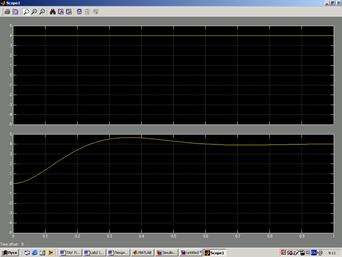
Рис.2.2.

В отличии от динамики, рассматривающей процессы протекающие в системе

во времени, статика изучает состояние покоя или равновесия. В этом случае

отсутствует временной фактор.

Из уравнения динамики (2.1), приравняв нулю все производные (так как режим установившейся), нетрудно получить уравнение статики системы

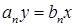, (2.2)

где 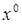- постоянная входная величина, 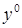- установившееся значение выходной величины.

Из уравнения статики можно получить статическую характеристику системы, представляющую собой зависимость выходной величины от входной в статическом режиме

.

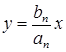Представим статическую характеристику в виде графика Рис.2.3.

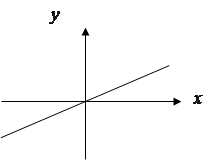
Рис.2.3.

Статическая характеристика может быть получена экспериментально путем подачи на вход системы постоянных воздействий и измерения установившихся значений выходных величин.