Вида записи системы уравнений.

Обычный, матричный и векторный виды записи системы уравнений:

, ,

.

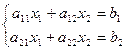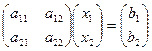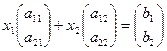Основная (А) и расширенная матрица (С).

, .

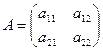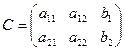Определение. Если существует хотя бы одно решение (то есть набор 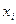, обращающий в тождества все уравнения) то система называется совместной, а если решения не существует, то несовместной, или противоречивой.

Слово «совместная» система означает, что уравнения совместны между собой, не противоречат друг другу. Примеры:

Совместная: 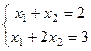есть решение (1,1).

Несовместная 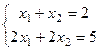если вычесть из 2-го уравнения удвоенное первое, получим противоречие: 0=1. А вот если в правой части 2-го уравнения было бы 4, а не 5, то система была бы совместной.

Две системы линейных уравнений называются эквивалентными, если множество их решений совпадает.

Определение.Если решение системы линейных уравнений единственно, то она называется определённой, если не единственно, то неопределённой.

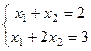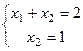Определённая: экв. решение (1,1).

Неопределённая: 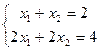Решения: (1,1) или (2,0) или (0,2) или (3,-1) или (4,-2), их бесконечно много. Фактически 2-е уравнение лишнее, а из 1-го следует 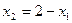. Что бы мы ни подставляли вместо 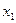, найдётся 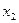. Единственного точного решения как такового здесь нет, их бесконечно много. Запись 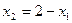здесь называется общим решением, а переменная 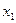, которую перенесли вправо и можем свободно задавать - свободной переменной.

Теорема Кронекера-Капелли о совместности системы уравнений.

Система линейных уравнений совместна тогда и только тогда, когда 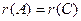(ранг основной матрицы равен рангу расширенной матрицы).

Доказательство.

Необходимость. Обозначим столбцы расширенной матрицы: 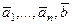. Пусть система совместна. Тогда существует решение, то есть такой набор чисел 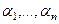, что .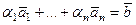

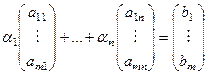
Тогда система, состоящая из векторов 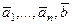, линейно зависима, причём 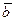не принадлежит её базису (он выражен через остальные). Тогда при добавлении вектора 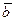ранг системы векторов не увеличивается на 1, а значит, при добавлении данного столбца не увеличивается и ранг матрицы, то есть .

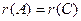Достаточность. Если 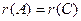, то базисный минор расширенной матрицы не пересекается с последним столбцом, а значит, в системе векторов 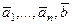, вектор 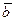не принадлежит базису системы. Тогда его можно линейно выразить через остальные, то есть 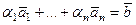, что означает, что 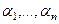- решение системы, она совместна.

Пример. Рассмотрим систему и её расширенную матрицу:

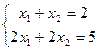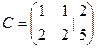
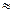
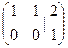, . Если рассматривать основную матрицу (до черты) там ранг = 1, потому что во 2-й строке только нули. А если всю расширенную матрицу, то там есть невырожденный минор 2-го порядка: 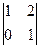. Ранги основной и расширенной матриц не совпадают.

Геометрический смысл при n=2.

Рассмотрим систему из 2 уравнений и 2 неизвестных: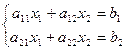

Её геометрический смысл. Каждое из уравнений задаёт некоторую прямую в плоскости. Прямые могут:

1. пересекаться в одной точке (решение единственно), в этом случае система совместная и определённая.

2. совпадать (решений бесконечно много), в этом случае система совместная, но неопределённая.

3. быть параллельны (нет решений) - система несовместна.