Виды уравнений регрессии

Простейший случай представляет собой простая линейная регрессия (парная корреляция), где рассматривается зависимость между двумя показателями: показателем результатов (у) и одним фактором (х), от которого зависит этот показатель. Такие модели называются однофакторными. Форма зависимости может быть линейной и нелинейной.

В исследованиях наиболее часто встречаются шесть следующих видов уравнений регрессии:

1) 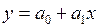– линейная;

2) 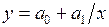– гиперболическая;

3) 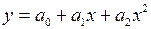– квадратичная, 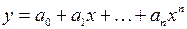– полиномиальная;

4) 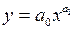– степенная;

5) 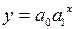– показательная;

6) 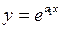– экспоненциальная.

Для измерения совместного влияния ряда показателей-факторов на исследуемую величину строятся модели множественной корреляции. Функция регрессии в общем случае запишется y = f (x₁, x₂, … , x_n).

Замена корреляционной зависимости на функциональную может привести к искажению отображения влияния факторов на результат. Поэтому общая задача регрессионного анализа состоит в определении такого вида и параметров уравнения регрессии, при которых наиболее точно представляется корреляционная зависимость.

При проведении регрессионного анализа необходимо выполнить, по крайней мере, следующие этапы работ:

1) определить показатели результатов производства и набор факторов, на них влияющих;

2) собрать статистические данные по этим показателям;

3) выбрать функцию для построения уравнения регрессии;

4) рассчитать значения коэффициентов (параметров) уравнения регрессии;

5) оценить надежность рассчитанных коэффициентов уравнения регрессии;

6) определить надежность оценок, полученных в результате использования уравнения регрессии;

7) провести анализ показателей, вытекающих из полученных расчетов.

Надежность оценок результирующего показателя 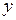, полученных в результате использования уравнения регрессии y = f (x₁, x₂, … , x_n), показывает, насколько эти оценки точнее, чем среднее значение 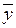случайной величины результирующего показателя. Надежность указанных оценок зависит от качества исходной информации и от качества уравнений регрессии.