Формулы преобразования треугольника (D) сопротивления в звезду (U).

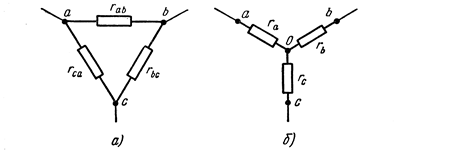
Преобразование треугольника сопротивлений в эквивалентную звезду. При расчете электрических цепей, которые не удается свести к одному результирующему сопротивлению путем замены последо­вательно и параллельно соединенных сопротивлений их эквивалент­ными величинами, приходится прибегать к более сложным преобра­зованиям. В частности, если в цепи встречается замкнутый контур из трех сопротивлений r_ab , r_bc и r_ca , образующих стороны треуголь­ника (рис.а), то эти сопротивления заменяют тремя сопротив­лениями r_a ,r_b и r_c , соединенными в одной узловой точке О и образую­щими трехлучевую звезду (рис. б).

Это преобразование должно быть эквивалентным, т. е. сопротив­ления между точками цепи a и b, b и c, c и a должны быть соответст­венно одинаковыми в обоих видах соединений:

, , .

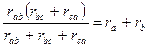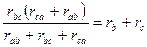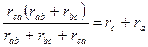Решая эти три уравнения относительно r_a , r_b, r _c находим

, , .

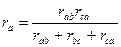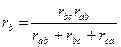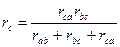При обратном переходе от трехлучевой звезды сопротивлении к эквивалентному треугольнику сопротивления r_{ab ,} r_bc и r_ca вы­ражают через сопротивления r_a, r_b и r_c:

, , .

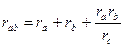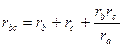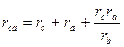Отметим, что указанные преобразования могут быть применены только в тех случаях, когда в замкну­том треугольнике сопротив­лений или в трехлучевой звезде отсутствуют источ­ники энергии (э. д.с.).

При преобразовании D вU и наоборот должна соблюдаться полная эквивалентность, т.е. U_abD=U_abU

I_abD=I_abU

ÞR_abD=R_abU (*)

U_abD= U_abU

Соотношение (*)не должно нарушаться, даже если в одном из узлов произошел обрыв.