I.7.3 ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Преобразования Лоренца описывают переход от одной инерциальной системы отсчёта к другой при очень больших скоростях их относительного движения.
Уравнения, описывающие преобразования координат и времени события при переходе из одной инерциальной системы отсчёта в другую, должны учитывать постоянство скорости света.
А. Преобразование пространственных координат
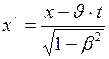 ;
; 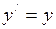 ;
; 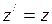 , (I.160)
, (I.160)
где 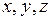 - пространственные координаты относительно системы
- пространственные координаты относительно системы  ;
;
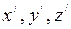 - пространственные координаты относительно системы
- пространственные координаты относительно системы 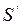 ;
;
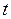 - время, измеренное в системе
- время, измеренное в системе  ;
;
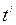 - время, измеренное в системе
- время, измеренное в системе 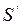 ;
;
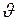 - скорость системы
- скорость системы 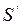 в направлении оси
в направлении оси 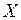 , измеренная в системе
, измеренная в системе  ;
;
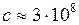 м/с – скорость света в вакууме;
м/с – скорость света в вакууме;
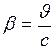 .
.
При 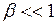 , т.е.
, т.е. 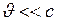 формула (I.160) переходит в формулу (I.157).
формула (I.160) переходит в формулу (I.157).
В. Преобразование времени
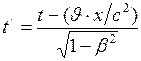 , или
, или 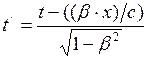 ; (I.161)
; (I.161)
При 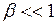 , т.е.
, т.е. 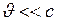 формула (I.161) переходит в формулу (I.156).
формула (I.161) переходит в формулу (I.156).
Так как пространственные координаты и время должны быть действительными величинами, относительная скорость двух инерциальных систем отсчёта не может превышать скорости света в вакууме.
Отметим, что Эйнштейн приходит к преобразованиям (I.160) и (I.161), исходя только из своих двух общих постулатов, в которых скорость света играет существенную роль.
Из формул преобразования мы видим, что скорость света в вакууме (в отсутствие гравитации) есть предельная скорость. Скорость материальной системы не может быть равна или больше 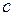 . Если бы это было не так, то под знаком корня получилась бы отрицательная величина и
. Если бы это было не так, то под знаком корня получилась бы отрицательная величина и 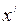 и
и 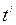 были бы мнимыми, т.е. никакого физического содержания мы этим формулам не придали бы.
были бы мнимыми, т.е. никакого физического содержания мы этим формулам не придали бы.
Кроме того, из формулы (I.161) мы видим относительность одновременности. Если два события одновременны в одной системе, то они, не одновременны в другой. С точки зрения принципа относительности можно принять за исходную систему не  , а
, а 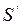 . Поскольку мы уже знаем лоренцево преобразование, то мы можем переписать его так, чтобы вместо
. Поскольку мы уже знаем лоренцево преобразование, то мы можем переписать его так, чтобы вместо 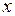 стояло
стояло 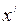 и наоборот, но только скорость тогда будет равна
и наоборот, но только скорость тогда будет равна 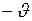 , если раньше она была
, если раньше она была 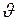 .
.
Таким образом, если мы исходим из системы 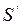 , то лоренцево преобразование можно представить в виде:
, то лоренцево преобразование можно представить в виде:
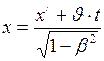 ;
; 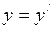 ;
; 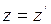 ,
, 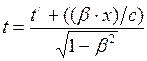 (I.162)
(I.162)
С другой стороны, мы могли бы просто вычислить 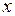 из линейных уравнений (I.160) и (I.161), и это привело бы к такому же результату. Таким образом, формулы преобразования такого рода удовлетворяют взаимности.
из линейных уравнений (I.160) и (I.161), и это привело бы к такому же результату. Таким образом, формулы преобразования такого рода удовлетворяют взаимности.
Дата добавления: 2016-09-06; просмотров: 2980;











