I.7.1 ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
В основе классической механики лежит принцип относительности Галилея (или механический принцип относительности): законы динамики одинаковы во всех инерциальных системах отсчёта. Этот принцип означает, что законы динамики неизменны относительно преобразований Галилея.
Преобразования Галилея связывают между собой различные кинематические величины, движущихся с некоторой скоростью в двух инерциальных системах отсчёта (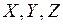 
и 
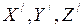) (рис.42).
Введём следующие обозначения:
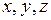- координаты относительно системы 
;
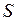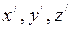- координаты относительно системы 
;
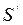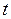- время, измеренное в системе ;
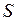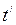- время, измеренное в системе ;
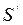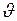- скорость системы 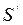в направлении оси 
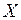, измеренная в системе ;
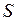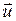- скорость тела в системе ; 
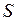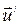- скорость тела в системе ;
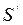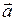- ускорение тела в системе ; 
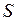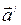- ускорение тела в системе .
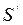А. Преобразование времени
В обеих системах отсчёта время течёт одинаково, т.е.
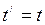. (I.156)
В. Преобразование пространственных координат
Пространственные координаты точки в обеих системах различаются на величину пути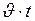 
, пройденного системой 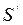в направлении оси 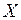за время :
; 
; 
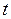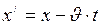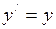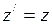(I.157)
.
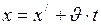С. Преобразование скоростей
Скорости тела 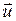различаются в обеих системах на величину скорости системы 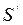в направлении оси :
; 
; 
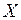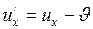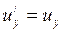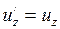; (I.158)
,
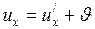где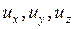 
- составляющие скорости 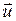, а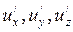 
- составляющие скорости .
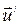D. Преобразование ускорений
Ускорения тел в направлении оси 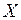в обеих системах одинаковы, поскольку при 
:
; 
; 
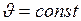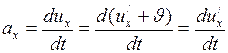
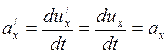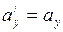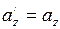, (I.159)
где 
- составляющие 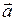и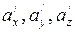 
- составляющие .
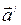Так как ускорения тел в обеих системах одинаковы, то и уравнение движения классической механики (второй закон Ньютона) не меняет своего вида при переходе от одной инерциальной системы к другой.
Кроме того, при переходе к инерциальной системе, движущейся с некоторой скоростью относительно другой системы, остаются инвариантными(неизменными) следующие величины: времена и ускорения. Скорости, напротив, изменяются по величине и направлению (если они не совпадают с направление оси ).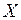
Дата добавления: 2016-09-06; просмотров: 2781;
Поиск по сайту
Узнать еще
- I.7.3 ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
- II.7.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
- Автоматические преобразования типов объектов
- Аналитический сигнал и преобразования Гильберта
- Аналого-цифровые преобразователи: назначение, ошибки преобразования, способы уменьшения динамических ошибок преобразования. Виды АЦП, сравнительная оценка.
- Аппаратный механизм преобразования виртуального адреса в физический
- В процессе этого преобразования мы получаем изображение, которое в той или иной мере похоже на оригинал.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
