Кривые второго порядка

Определение 3.4.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой–либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух перемен.

Эллипс.

Определение 3.4.1.1. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная равная 2а, где 2a > F₁F₂.

	Рис. 3.7. Вывод уравнения эллипса

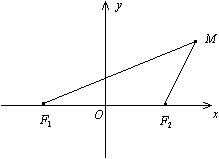
Выведем уравнение эллипса, выбрав декартову систему координат так, чтобы ось Ох совпала с прямой F₁F₂, начало координат – с серединой отрезка F₁F₂. Пусть длина этого отрезка равна 2с, тогда в выбранной системе координат. Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F₁ и F₂ равна 2а.

Тогда r₁ + r₂ = 2a, но 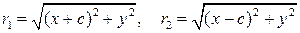, поэтому

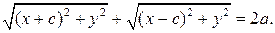Введя обозначение b² = a² – c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:

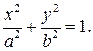(3.37)

Определение 4.4.1.2. Эксцентриситетом эллипса называется величина е=с/а.

Определение 4.4.1.3. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (3.37), а уравнением второй степени другого вида.

Свойства эллипса:

1. Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a > 2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2. Весь эллипс содержится внутри прямоугольника 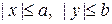и в первой четверти .

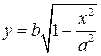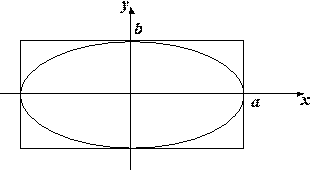
Рис. 3.8. Эллипс

3. Эксцентриситет эллипса e < 1.

Действительно,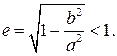

4. Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е < 1, следовательно, а/е > a).

5. Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

6. Если полуоси эллипса равны (a=b), то эллипс становится окружностью, радиус которой равен его полуосям, эксцентриситет окружности e=0, а фокусы совпадают.

7. Параметрическое уравнение эллипса: .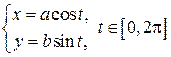

Действительно .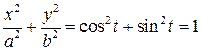

Гипербола.

Определение 3.4.2.1. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная равная 2а, где 2a< F₁F₂.

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|r₁ – r₂| = 2a, откуда 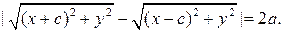Если обозначить b² = c² – a², отсюда можно получить

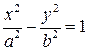– каноническое уравнение гиперболы. (3.38)

Определение 3.4.2.2. Эксцентриситетом гиперболы называется величина е = с / а.

Определение 3.4.2.3. Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

Свойства гиперболы:

1. Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2. Ветви гиперболы имеют две асимптоты, определяемые уравнениям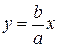и

и .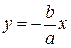

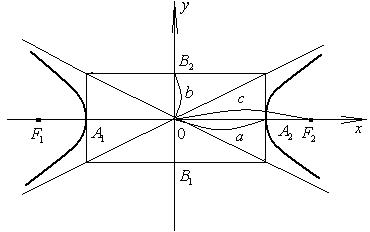
Рис.3.9. Гипербола

3. Наряду с гиперболой (3.38) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

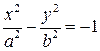, (3.39)

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот (рис. 3.10)

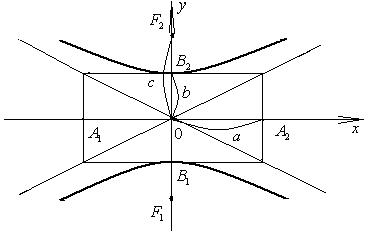
Рис. 3.10. Сопряженная гипербола, пересекающая ось Oy

4. гипербола лежит вне полосы –b<y<b.

5. Эксцентриситет гиперболы e > 1.

6. Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

7. Параметрические уравнения гиперболы

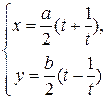или

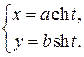
Парабола.

Определение 3.4.3.1. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой.

Точка F называется фокусом параболы, а прямая – ее директрисой.

	Рис. 3.11. Вывод уравнения параболы

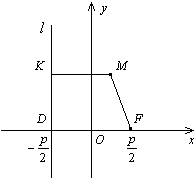
Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина перпендикуляра FD, опущенного из фокуса на директрису, а координатные оси располагались параллельно и перпендикулярно директрисе.

Пусть длина отрезка FD равна р. Тогда из равенства r = d следует, 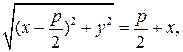поскольку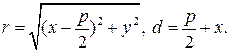

Алгебраическими преобразованиями это уравнение можно привести к виду

y² = 2px, (3.40)

называемому каноническим уравнением параболы. Величина р называется параметром параболы.

Свойства параболы:

1. Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2. Вся парабола расположена в правой полуплоскости плоскости Оху (рис. 3.12).

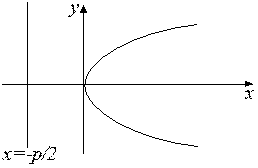
Рис. 3.12. Парабола

3. Если уравнение параболы имеет вид 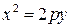, , 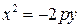то её график имеет вид

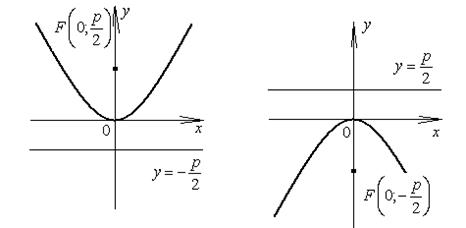
Рис. 3.13. Варианты параболы

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e < 1), гиперболу (при e > 1) или параболу (при е = 1).