Поверхности второго порядка

Определение 3.5.1 Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:

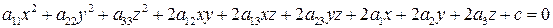(3.50)

- уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.

При переходе к ортонормированному базису собственных векторов исчезают все смешанные произведения переменных, и можно получить следующую классификацию поверхностей второго порядка:

I. Если 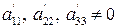, то уравнение преобразуется к виду

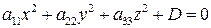(3.51)

и его можно привести к одному из следующих видов:

1) если 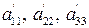– одного знака, то уравнение (3.51) есть уравнение эллиптического типа и приводится к канонической форме

а) если D такого же знака

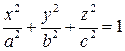(3.52)

- каноническое уравнение эллипсоида (рис. 3.16).

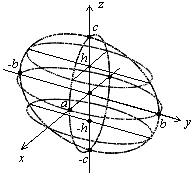
Рис. 3.16. Эллипсоид

Замечание. Если хотя бы два коэффициента совпадают, эллипсоид называется эллипсоидом вращения и представляет собой поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Если все коэффициенты равны, уравнение (3.51) становится уравнением сферы.

Пример 3.10.

Нарисуйте сферу .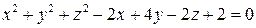

Решение.

Выделив полные квадраты, получим 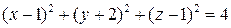. Значит, центром сферы является точка М₀(1; –2; 1), радиус сферы равен 2 (рис. 3.16).

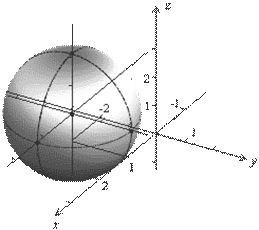
Рис. 3.17. Сфера

б) если D = 0, получим следующее уравнение 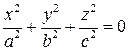(3.53)

- уравнение задает точку в пространстве или мнимый конус;

в) если D другого знака, уравнение имеет вид 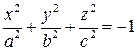(3.54)

- пустое множество или мнимый эллипсоид.

2. Если 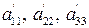разных знаков, уравнение (3.51) приводится к виду:

а) 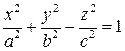- уравнение однополостного гиперболоида (3.55)

Рис. 3.18. Однополостный гиперболоид

б) 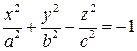- уравнение двуполостного гиперболоида (3.56)

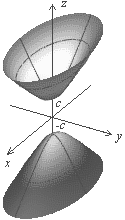
Рис. 3.19. Двуполостный гиперболоид

в) 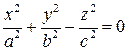- уравнение конуса второго порядка (3.57)

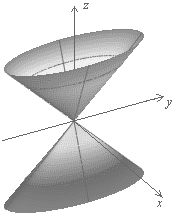
Рис. 3.20. Конус

II. Одно из чисел 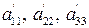равно 0. Например, 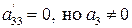. При этом с помощью преобразований координат можно получить следующие формы уравнения (3.50):

а) 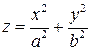- уравнение эллиптического параболоида (3.58)

Рис. 3.21. Эллиптический параболоид

Если a=b, то сечения плоскостями, параллельными плоскости Oxy, являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости Oyz, вокруг оси Oz (рис. 3.22).

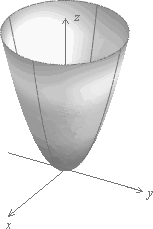
Рис. 3.22. Параболоид вращения

б) 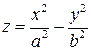- уравнение гиперболического параболоида (3.59)

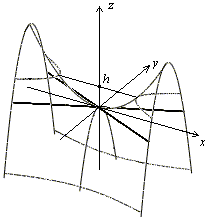
Рис. 3.23. Гиперболический параболоид (седло)

III. Если одно из чисел 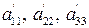равно 0. Например, 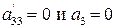, тогда получаем такую же классификацию, как у кривых второго порядка на плоскости. Рассмотрим реально существующие поверхности:

а) 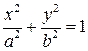- эллиптический цилиндр (рис. 3.24). (3.60)

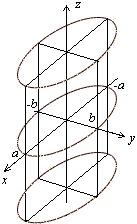
Рис.3.24. Эллиптический цилиндр

б) 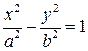- гиперболический цилиндр (рис. 3.25). (3.61)

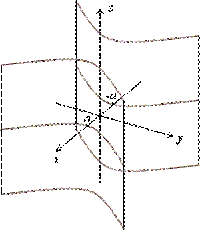
Рис. 3.25. Гиперболический цилиндр

в) 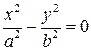- пара пересекающихся плоскостей. (3.62)

г) 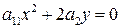параболический цилиндр (рис. 3.26). (3.63)

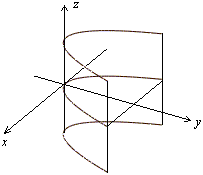
Рис. 3.26. Параболический цилиндр

д) 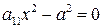- пара параллельных плоскостей. (3.64)

е) 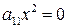- пара слипшихся плоскостей. (3.65)