Классификация кривых второго порядка.

I. Рассмотрим уравнение (3.46)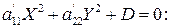

а) если 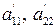одного знака, уравнение называется уравнением эллиптического типа;

1) если D имеет другой знак, то при делении на –D получаем

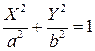– каноническое уравнение эллипса;

2) если D=0, уравнение 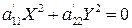имеет единственное решение 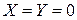, определяющее точку на плоскости или пару мнимых пересекающихся прямых;

3) если знак D противоположен знаку 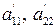, уравнение после деления на D примет вид:

.

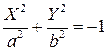Множество его решений пусто (иногда это пустое множество называют мнимым эллипсом).

б) если 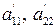разных знаков, то (3.47) называется уравнением гиперболического типа;

1) при 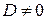оно сводится к одному из двух видов:

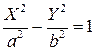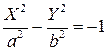или , в зависимости от знака D. Оба этих уравнения определяют гиперболу.

2) при D=0 получаем уравнение 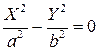эквивалентное двум линейным уравнениям 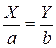и 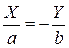, задающим пару пересекающихся прямых.

II. Рассмотрим уравнение (3.48), после деления на 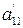получим уравнение 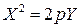, определяющее параболу.

III. Рассмотрим уравнение (3.49):

1) если 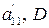разных знаков, то его можно привести к уравнению 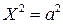или 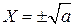, задающему пару параллельных прямых;

2) если 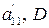одного знака, то уравнение можно привести к виду, не имеющему решений и, следовательно, не определяющему никакого геометрического образа (иногда это пустое множество называют пара мнимых параллельных прямых);

3) если D = 0, то уравнение преобразуется к уравнению 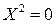, определяющему одну прямую (или пару слипшихся прямых).

Пример 3.9.

Найти каноническое уравнение линии второго порядка:

5x² + 12xy – 22x – 12y – 19 = 0.

Решение.

Найдём угол поворота по формуле (3.45)

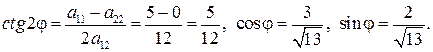
Осуществим поворот по формулам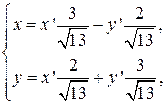

тогда уравнение примет вид:

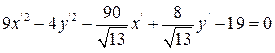или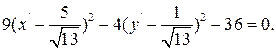

После параллельного переноса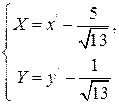

получим 9Х²–4У²=36 или .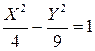

Это уравнение гиперболы с полуосями, соответственно, 2 и 3 и центром ( 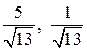). Координаты центра в исходной системе координат х = 1, y = 1.