Прямая в пространстве.

Замечание. Прямую в пространстве невозможно задать одним уравнением. Для этого требуется система двух или более уравнений.

Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z + D₂ = 0, где коэффициенты A₁, B₁, C₁ и A₂, B₂, C₂ не пропорциональны:

A₁x + B₁y + C₁z + D₁ = 0,

A₂x + B₂y + C₂z + D₂ = 0. (3.28)

Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.

Составим уравнения прямой, проходящей через точку М₀(x₀,y₀,z₀) параллельно вектору s=(m,n, p).

Определение 3.3.5.1. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.

Для любой точки М(x,y,z), лежащей на данной прямой, вектор

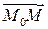= (x – x₀, y – y₀, z – z₀) коллинеарен направляющему вектору s. Поэтому имеют место равенства

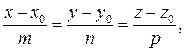(3.29)

называемые каноническими уравнениями прямой в пространстве.

В частности, если требуется получить уравнения прямой, проходящей через две точки М₁(х₁, у₁, z₁) и M₂(x₂, y₂, z₂), направляющим вектором такой прямой можно считать вектор 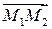= (x₂ – x₁, у₂ – y₁, z₂ – z₁}, и уравнения (3.28) принимают вид:

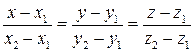(3.30)

это уравнения прямой, проходящей через две данные точки.

Если же принять каждую из равных дробей в уравнениях (3.29) за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:

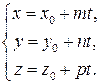(3.31)

Для того чтобы перейти от уравнений (3.28) к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор этой прямой и координаты любой точки, принадлежащей ей.

Направляющий вектор прямой ортогонален нормалям к обеим плоскостям, следовательно, он коллинеарен их векторному произведению. Поэтому в качестве направляющего вектора можно выбрать n₁´n₂ или любой вектор с пропорциональными координатами.

Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно (обычно z = 0), а две остальные найти из уравнений (3.28).

Пример 3.8.

Составить канонические уравнения прямой.

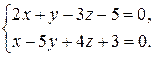
Решение.

Найдем n₁´n₂, n₁ = (2,1,–3), n₂ = (1,–5,4). Тогда n₁·n₂ = (–11, –11, –11). Следовательно, направляющим вектором прямой можно считать вектор (1,1,1).

Будем искать точку на прямой с координатой z₀ = 0. Для координат х₀ и у₀ получим систему уравнений 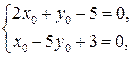откуда х₀ = 2, у₀ = 1. Теперь можно составить канонические уравнения прямой

.

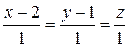Параметрические уравнения той же прямой имеют вид

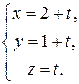
Замечание. Если какая–либо из координат направляющего вектора равна 0, то предполагается, что для любой точки прямой числитель соответствующей дроби в канонических уравнениях тоже равен 0.