Векторы в пространстве. Основные определения.

Определение 1. Вектором в пространстве называется направленный отрезок.

Таким образом, векторы в отличие от скалярных величин имеют две характеристики: длину и направление. Будем обозначать векторы символами 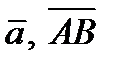, или а.

(Здесь А и В – начало и конец данного вектора (рис.1)) а В

Длина вектора обозначается символом модуля: 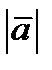. А рис.1

Различают три вида векторов, задаваемых отношением равенства между ними:

Закрепленные векторы называются равными, если у них совпадают начала и концы соответственно. Примером такого вектора является вектор силы.
Скользящие векторы называются равными, если они расположены на одной прямой, имеют одинаковые длины и направления. Примером таких векторов является вектор скорости.
Свободные или геометрические векторы считаются равными, если они могут быть совмещены с помощью параллельного переноса.

В курсе аналитической геометрии рассматриваются только свободные векторы.

Определение 2. Вектор, длина которого равна нулю, называется нулевым вектором, или ноль –

вектором.

Очевидно, начало и конец нулевого вектора совпадают. Нулевой вектор не имеет определенного направления или имеет любое направление.

Определение 3. Два вектора, лежащих на одной прямой или параллельных прямых называются

коллинеарными (рис.2). Обозначают: 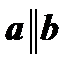. a

b

Нулевой вектор можно считать коллинеарным любому. рис.2

Определение 4.Два коллинеарных и одинаково направленных вектора называются

сонаправленными. Обозначают: .

Теперь можно дать строгое определение равенства свободных векторов:

Определение 5.Два свободных вектора называются равными, если они сонаправлены и имеют

одинаковую длину.

Определение 6.Три вектора, лежащих в одной или параллельных плоскостях называются

компланарными.

Два перпендикулярных вектора называют взаимно ортогональными: .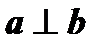

Нулевой вектор можно считать ортогональным любому.

Определение 7.Вектор единичной длины называется единичным вектором или ортом.

Орт, сонаправленный ненулевому вектору а называют ортом вектора а : e_a .

§2. Линейные операции над векторами.

На множестве векторов определены линейные операции: сложение векторов и умножение вектора на число.

Дата добавления: 2021-10-28; просмотров: 267;