Взаимное положение прямых в пространстве.

Задание и изображение прямой на комплексном чертеже

Для того чтобы задать прямую, необходимо и достаточно задать две ее точки.

А2

а1

В1

а2

В2

X12

А1

Прямая относительно плоскостей проекций может занимать различные положения:

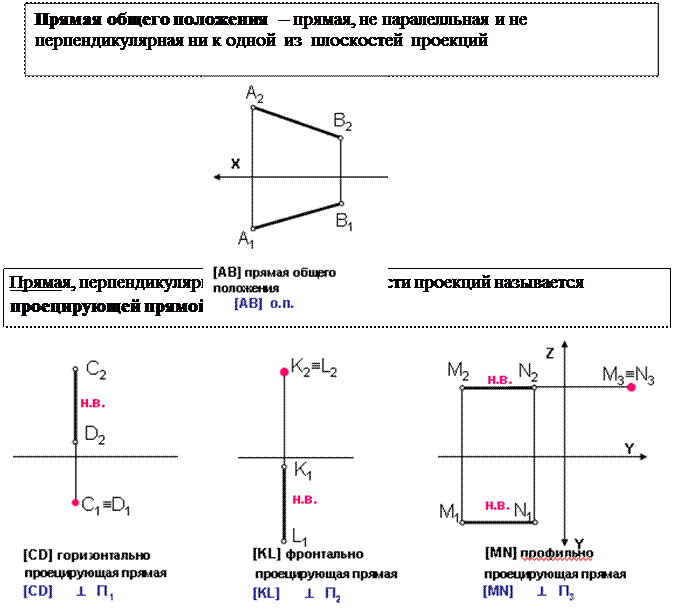
- Прямая общего положения

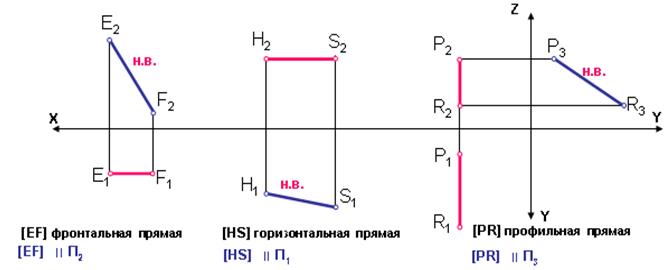
- Прямая частного положения (проецирующая прямая ипрямая уровня)

		Прямая, параллельная какой-либо плоскости проекций называетсяпрямой уровня.

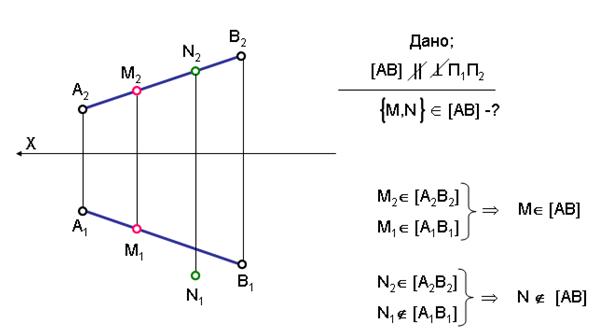
2.Принадлежность точки к прямой

Если точка принадлежит линии, то проекции точки принадлежат соответствующим проекциям этой точки

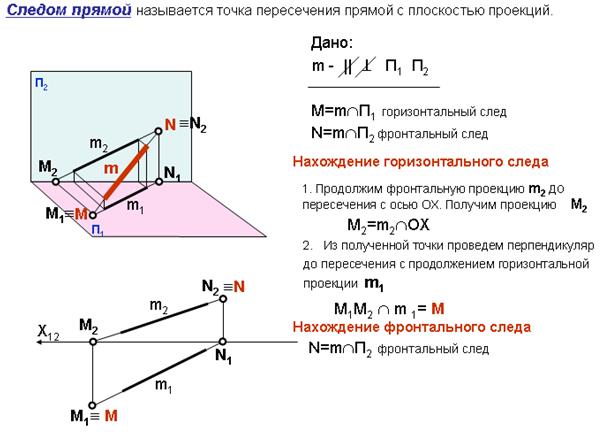
Следы прямой

Взаимное положение прямых в пространстве.

Прямые линии в пространстве могут пересекаться, быть взаимно параллельными или скрещиваться.

Параллельные прямые - прямые, лежащие в одной плоскости и не имеющие общих точек.

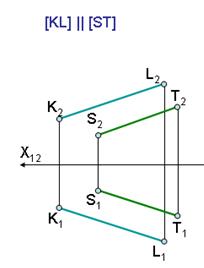Одноименные проекции параллельных прямых всегда параллельны.

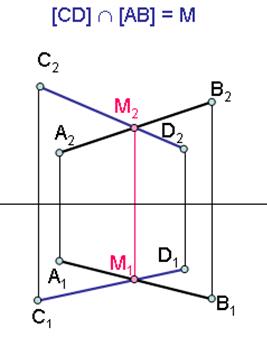
Пересекающиеся прямые - прямые, лежащие в одной плоскости и имеющие общую точку пересечения.

Проекции точки пересечения прямых всегда находятся на одной линии связи.

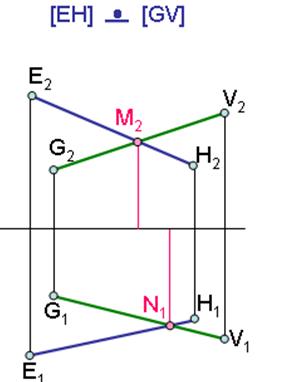
Скрещивающиеся прямые - прямые, не лежащие в одной плоскости.

Проекции точек пересечения проекций прямых никогда не находятся на одной линии связи.

С помощью конкурирующих точек определяют видимость тех или иных

геометрических элементов относительно плоскостей проекций.

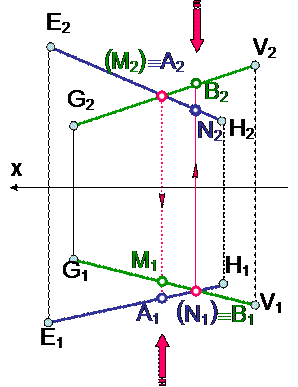На рис. изображены две пары конкурирующих точек: фронтально конкурирующие(МºА) и горизонтально конкурирующие точки (NºB).

Смотрим по направлению стрелки.

- Из двух фронтально конкурирующих точек видна будет та точка, которая расположена ближе к наблюдателю, т.е. наиболее удаленная от фронтальной плоскости проекций. (точка A– видимая)

- Из двух горизонтально конкурирующих точек видна будет та точка, которая расположена выше относительно горизонтальной плоскости проекций ( точка B- видимая).