Из истории возникновения и развития геометрии. Свойства геометрических фигур на плоскости и в пространстве.

Опр. 1. Геометрической фигуройФ называется всякое непустое множество точек.

Если все точки геометрической фигуры принадлежат одной плоскости, то она называется плоской.

Рассмотрим определения некоторых плоских фигур.

Опр. 2. Лучом называется множество точек прямой, лежащих по одну сторону от некоторой точки этой прямой.

Опр. 3. Угол– это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи наз. сторонами угла, а их общее начало – его вершиной.

Обозначают угол: ∠А, ∠(k,l), ∠АВС.

Опр. 4. Треугольникомназывается геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.

Треугольники называются равными, если у них соответст­вующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствую­щих сторон.

Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.

Опр. 5. Четырехугольникомназывается фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не долж­ны пересекаться. Данные точки называются вершинами четы­рехугольника, а соединяющие их отрезки - его сторонами.

Параллелограммомназывается четырехугольник, у которо­го противолежащие стороны параллельны.

Из множества параллелограммов выделяют прямоугольники и ромбы.

Ромбомназывается параллелограмм, у которого все стороны равны.

Прямоугольникомназывается параллелограмм, у которого все углы прямые.

Прямоугольникомназывается четырехугольник, у которого все углы прямые ( определение из курса математики начальной школы).

Квадратом называется прямоугольник, у которого все стороны равны.

Квадратом называется ромб, у которого все углы прямые.

Трапециейназывается четырехугольник, у которого только две противолежащие стороны параллельны.

Эти параллельные стороны называются основаниями тра­пеции. Две другие стороны называются боковыми.

Многоугольником называется замкнутая ломаная, если ее звенья не лежат на одной прямой.

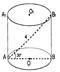
Окружностьюназывается фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки, которая называется центром.

Всякая конечная замкнутая область трехмерного пространства называется телом.

Примерами тел могут служить пространственные фигуры.

Многогранник - это ограниченное тело, поверхность которого состоит из конечного числа многоугольников.

Выпуклый многогранниклежит по одну сторону от каждого из ограничи­вающих его многоугольников. Многоугольник на поверхно­сти многогранника называется его гранью. Стороны граней называются ребрами многогранника, а вершины граней - вер­шинами многогранника.

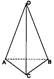
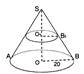
Простейшие многогранники - это призма и пирамида.

Призмойназывается многогранник, у которого две грани, называемые основаниями призмы, равны и их соответственные стороны параллельны, а остальные грани - параллело­граммы, у каждого из которых две стороны являются соответ­ственными сторонами оснований.

Призма называется прямой,если ее боковые ребра перпен­дикулярны основанию. Прямая призма называется правильной,если ее основанием является правильный многоугольник.

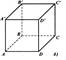
Призма, у которой основание- параллелограмм, называется параллелепипедом.