Уравнение касательной
Рассмотрим случай касательной к овальной квадрике, (D = 0).
4∙(АТ∙QТ∙В)²-4∙(АТ∙Q∙А)∙(ВТ∙Q∙В)=0  (АТ∙QТ∙В)²-(АТ∙Q∙А)∙(ВТ∙Q∙В)=0.
(АТ∙QТ∙В)²-(АТ∙Q∙А)∙(ВТ∙Q∙В)=0.
Если точку А фиксировать, а точку В сделать переменной тогда уравнение касательной к квадрике, проведенной из точки А, будет следующим: (АТ∙QТ∙Х) ² - ( АТ∙Q∙А)∙( Х Т∙Q∙Х) =0 (**)
Фактически это уравнение является квадратичной формой и в то же время уравнением прямой, то есть распадается на прямые. Проанализируем это уравнение для случая, когда точка А принадлежит квадрике и не принадлежит квадрике.
· А 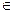 КВП
КВП  АТ∙Q∙А=0
АТ∙Q∙А=0  (АТ∙QТ∙Х)²=0 - квадратичная форма (**) распалась на две совпавшие прямые. Т.о. АТ∙QТ∙Х =0 - уравнение касательной.
(АТ∙QТ∙Х)²=0 - квадратичная форма (**) распалась на две совпавшие прямые. Т.о. АТ∙QТ∙Х =0 - уравнение касательной.
· А 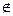 КВП.
КВП.
(АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = 0 - ранг этой квадратичной формы не может равняться 3 потому, что это прямые, а значит квадратичная форма должна быть вырожденной. Так же ранг этой квадратичной формы не может быть равен 1. Докажем это от противного.
Пусть ранг (**) равен 1, тогда она распадается на две совпавшие прямые
(АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = (и∙Х)²
 ХТ∙Q∙Х=
ХТ∙Q∙Х= 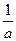 ((АТ∙QТ∙Х)² -(и∙Х)²)=
((АТ∙QТ∙Х)² -(и∙Х)²)= 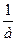 ((АТ∙QТ∙Х)- и∙Х) ((АТ∙QТ∙Х)+и∙Х)
((АТ∙QТ∙Х)- и∙Х) ((АТ∙QТ∙Х)+и∙Х)
 овальная квадрика ХТ∙Q∙Х распалась на линейные множители, на прямые - это противоречие. Т.о. ранг (**) равен 2, т.е. это или две пересекающиеся прямые или две мнимые прямые пересекающиеся в одной действительной точке.
овальная квадрика ХТ∙Q∙Х распалась на линейные множители, на прямые - это противоречие. Т.о. ранг (**) равен 2, т.е. это или две пересекающиеся прямые или две мнимые прямые пересекающиеся в одной действительной точке.
Вывод: Если точка принадлежит квадрике, то через неё можно провести только одну касательную. Если точка не принадлежит квадрике, то касательных или две или ни одной.

Определение: Точка называется внешней относительно квадрики, если через нее можно провести две касательных и внутренней, если касательных нет.
Лемма. Пусть дана овальная квадрика х1²+х2²-х3²=0 и точка 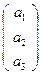 . Точка является внутренней точкой овальной квадрики тогда и только тогда, когда а1²+а2²-а3² < 0 (если а1²+а2²-а3² > 0 - внешней).
. Точка является внутренней точкой овальной квадрики тогда и только тогда, когда а1²+а2²-а3² < 0 (если а1²+а2²-а3² > 0 - внешней).
Доказательство. (Самостоятельно).
Задача. Дана квадрика 2∙х1²+х3²-2∙х1∙х2-2∙х1∙х3=0.
Найти уравнения касательных к квадрике, проходящих через точки А 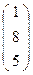 , В
, В 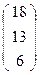 .
.
Решение. Матрица квадрики Q= 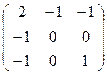 .
.
АТ∙Q∙А=(1:8:5)∙ 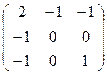 ∙
∙ 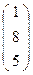 =(-11:-1:4)∙
=(-11:-1:4)∙ 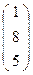 =1
=1  А
А 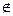 КВП,
КВП,
Применим формулу (**) (АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = 0.
АТ∙Q∙Х=( 1: 8 : 5 )∙ 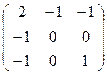 ∙
∙ 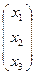 =(-11 : -1 : 4)∙
=(-11 : -1 : 4)∙ 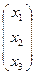
 11∙х1+ х2 - 4∙х3=0
11∙х1+ х2 - 4∙х3=0
(11∙х1 + х2 - 4∙х3 )² - 1∙(2∙х1² + х3² - 2∙х1∙х2 - 2∙х1∙х3 ) =
= 121∙х1² + х2² + 16∙х3² + 22∙х1∙х2 - 88∙х1∙х3 - 8∙х2∙х3 - 2∙х1² - х3² + 2∙х1∙х2 + 2∙х1∙х3 =
= 119∙х1² + х2² + 15∙х3² + 24∙х1∙х2 - 86∙х1∙х3 - 8∙х2∙х3 =
= х2² +2∙х2∙12∙х1 -2∙х2∙4∙х3 +144∙х1² +16∙х3² -2∙12∙х1∙4∙х3 -144∙х1² -16∙х3² +96∙х1∙х3 +119∙х1² +15∙х3² -86∙х1∙х3 =
= (х2 + 12∙х1 -∙4∙х3 )² - 25∙х1² - х3² + 10∙х1∙х3 = (х2 + 12∙х1 -∙4∙х3 )² - (5∙х1 - х3 )² =
= ((х2 + 12∙х1 - 4∙х3 ) - (5∙х1 - х3 ))∙((х2 + 12∙х1 - 4∙х3 ) + (5∙х1 - х3 ))=
= (х2 + 12∙х1 - 4∙х3 - 5∙х1 + х3 )∙(х2 + 12∙х1 - 4∙х3 + 5∙х1 - х3 )=
= (х2 +7∙х1 -3∙х3 )∙(х2 +17∙х1 -5∙х3) = (7∙х1 + х2 - 3∙х3 )∙(17∙х1 + х2 - 5∙х3) = 0.
Т.о. касательные: 7∙х1 + х2 - 3∙х3 = 0 и 17∙х1 + х2 - 5∙х3 = 0.
ВТ∙Q∙В=(18:13:6)∙ 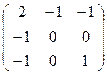 ∙
∙ 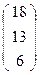 = (17:-18:-12) ∙
= (17:-18:-12) ∙ 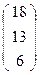 =0
=0  В
В  КВП.
КВП.
Уравнение касательной:
ВТ∙Q∙Х = ( 18 : 13 : 6 )∙ 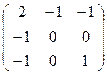 ∙
∙ 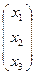 = 0
= 0  ( 17 : -18 : -12 )∙
( 17 : -18 : -12 )∙ 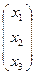 = 17∙х1 -18·х2 - 12∙х3 = 0.
= 17∙х1 -18·х2 - 12∙х3 = 0.
Полюс и поляра
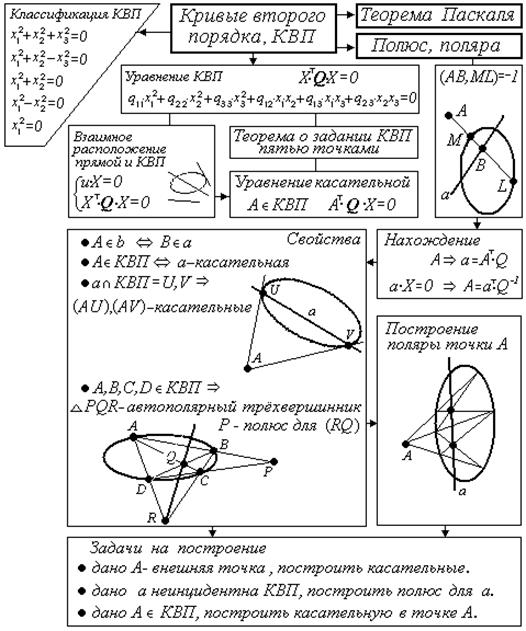
Рассмотрим овальную квадрику ХТ∙Q∙Х = 0 и точки А и В не принадлежащие квадрике.
 Пусть M и L точки пересечения квадрики и прямой (АВ).
Пусть M и L точки пересечения квадрики и прямой (АВ).
Определение: Если (AB,ML)=-1, то говорят что овальная квадрика гармонически разделяет пару АВ, или точки А и В гармонически сопряжены относительно овальной квадрики.
На прямой (АВ) рассмотрим репер R(A,B,M), тогда в этом репере и точки А 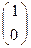 , В
, В 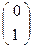 , М
, М 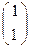 и пусть точка L
и пусть точка L 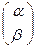 .
.
Если (AB,ML)= -1, тогда 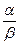 = -1
= -1  α = 1 и β = -1 , т.е. L
α = 1 и β = -1 , т.е. L 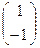 .
.
Таким образом, М = А+В и L = А – В.
Значит, для точек пересечения прямой (АВ) с квадрикой 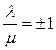 .
.
Но 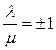 являются корнями уравнения λ²∙а + 2∙λ∙μ∙с + μ²∙b=0,
являются корнями уравнения λ²∙а + 2∙λ∙μ∙с + μ²∙b=0,
где а = АТ∙Q∙А, b = ВТ∙Q∙В, с = А Т∙Q∙В = ВТ∙Q∙А.
По теореме Виета сумма корней равна среднему коэффициенту, взятому с противоположным знаком: 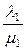 +
+ 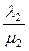 = - с
= - с  с = 0
с = 0  АТ∙Q∙В = ВТ∙Q∙А = 0 - условие гармонической сопряженности точек А и В относительно квадрики.
АТ∙Q∙В = ВТ∙Q∙А = 0 - условие гармонической сопряженности точек А и В относительно квадрики.
Фиксируем точку А 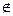 КВП. Рассмотрим все прямые проходящие через эту точку в каждом случае будет своя точка В гармонически сопряженная с А относительно овальной квадрики. Сделаем точку В переменной, по условию гармонической сопряженности точек относительно овальной квадрики получим: АТ∙Q∙Х =0 - это уравнение I степени, то есть прямая, причем это прямая единственна. Эту прямую будем называть полярой точки А. Если точка А
КВП. Рассмотрим все прямые проходящие через эту точку в каждом случае будет своя точка В гармонически сопряженная с А относительно овальной квадрики. Сделаем точку В переменной, по условию гармонической сопряженности точек относительно овальной квадрики получим: АТ∙Q∙Х =0 - это уравнение I степени, то есть прямая, причем это прямая единственна. Эту прямую будем называть полярой точки А. Если точка А 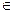 КВП, то уравнение АТ∙Q∙Х =0 определяет касательную к квадрике в точке А.
КВП, то уравнение АТ∙Q∙Х =0 определяет касательную к квадрике в точке А.
Определение: Полярой точки А называется прямая, состоящая из точек гармонически сопряженных с данной точкой относительно овальной квадрики.
Вывод: Полярой точки А является прямая, которая имеет уравнение: АТ∙Q∙Х =0 и
в случае А 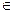 КВП является касательной к овальной квадрике,
КВП является касательной к овальной квадрике,
в случае А 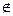 КВП состоит из точек гармонически сопряженных с точкой А относительно овальной квадрики.
КВП состоит из точек гармонически сопряженных с точкой А относительно овальной квадрики.
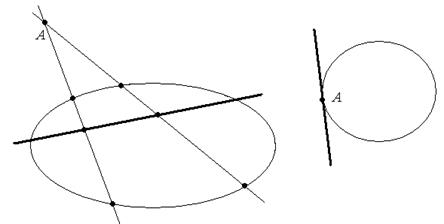
Определение:Уравнение АТ∙Q∙Х =0 называется уравнением поляры точки А относительно овальной квадрики.
Если уравнение прямой а∙Х=0, тогда λ∙а = АТ∙Q (с точностью до пропорциональности).
λ∙а =АТ∙Q  λ∙а∙Q-1 =АТ∙Q∙Q-1
λ∙а∙Q-1 =АТ∙Q∙Q-1  μ∙АТ= а∙Q-1 или μ∙А= Q-1 ∙аТ
μ∙АТ= а∙Q-1 или μ∙А= Q-1 ∙аТ
(Почему существуетQ-1 и почему (Q-1)Т= Q-1 ? )
Вывод: Для любой прямой существует точка, для которой эта прямая является полярой относительно квадрики.
Определение: Точка, для которой данная прямая относительно овальной квадрики является полярой, называется полюсом прямой.
Свойства:
1. Если точка А внешняя по отношению к овальной квадрике, то ее поляра проходит через точки касания касательных проведенных из точка А к КВП.
Доказательство. Координаты точек касания Х1 и Х2 находятся из системы 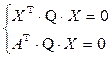 , первое уравнение это уравнение квадрики, второе уравнение это уравнение поляры, а значит это точки пересечения поляры и квадрики. □
, первое уравнение это уравнение квадрики, второе уравнение это уравнение поляры, а значит это точки пересечения поляры и квадрики. □
2. Если точка и прямая инцидентны, то их поляра и полюс тоже инцидентны.
Доказательство. Пусть а – поляра точки А и В - полюс прямой b,
значит λ∙а =АТ∙Q и μ∙В= Q-1 ∙bТ. Докажем, что А 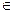 b
b  B
B 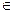 a.
a.
Уравнение прямой b∙Х = 0, тогда А 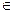 b
b  b∙А =0.
b∙А =0.
Найдем а∙В=(АТ∙Q)∙(Q-1∙b)=АТ∙(Q∙Q-1)∙bТ=АТ∙Е∙bТ=АТ∙bТ=(А∙b)Т=0 - это означает, что точка В лежит на прямой а. □
Замечание: Свойство 2 позволяет находить полюс прямой. Выбрав на данной прямой две любые точки и построив их поляры, точка их пересечения будет полюсом данной прямой.
Задача. Дана квадрика х1² - 2∙х2²+ 4∙х2∙х3 =0 . Найти уравнение поляры для А 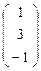 и координаты полюса прямой b: х1+х2–2∙х3=0.
и координаты полюса прямой b: х1+х2–2∙х3=0.
Решение. Q= 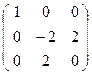
 Q-1=
Q-1= 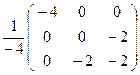
λ∙а=АТ∙Q=( 1: 3 :-1) ∙ 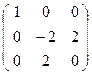 =(1 :-8: 6)
=(1 :-8: 6)  х1 -8∙х2+6∙х3=0.
х1 -8∙х2+6∙х3=0.
μ∙В=Q-1∙bТ= 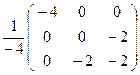 ∙
∙ 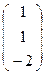 =
= 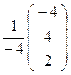
 В=
В=  .
.
Задача. Дана квадрика 2∙х1² + х3² - 2∙х1∙х2 -2∙х1∙х3 =0 . Найти уравнения касательных к квадрике из точки А 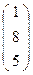 .
.
Решение. Воспользуемся свойством (1). Q= 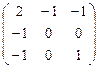 . Найдем уравнение поляры.
. Найдем уравнение поляры.
λ∙а = АТ∙Q=( 1: 8 : 5 )∙ 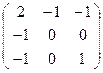 =( -11 : -1 : 4 )
=( -11 : -1 : 4 )  11∙х1 + х2 - 4∙х3 =0.
11∙х1 + х2 - 4∙х3 =0.
Найдем точки пересечения квадрики поляры.
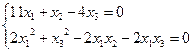

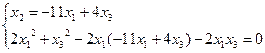

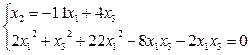

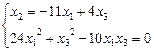

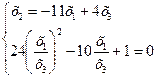

D=100–96 = 4 
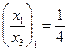 и
и 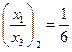 .
. 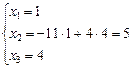 и
и 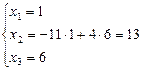

В 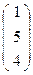 и С
и С 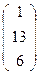 - точки пересечения поляры и квадрики, тогда прямые (АВ) и (АС) будут касательными.
- точки пересечения поляры и квадрики, тогда прямые (АВ) и (АС) будут касательными.
(АВ) : 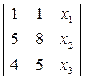 =0
=0  - 7∙х1 - х2 + 3∙х3 =0.
- 7∙х1 - х2 + 3∙х3 =0.
(АС) : 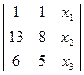 =0
=0  17∙х1 + х2 - 5∙х3 =0.
17∙х1 + х2 - 5∙х3 =0.
Определение: Трехвершинник называется автополярным относительно овальной квадрики, если каждая его вершина является полюсом противоположной стороны.
Замечание: Автополярных трехвершинников может быть много.
Теорема. Для того чтобы уравнение овальной квадрики было каноническим необходимо и достаточно, чтобы ΔЕ1Е2Е3 был автополярным относительно данной квадрики.
Доказательство. Необходимость:
Дано q11 ∙х1² + q22∙х2² + q33∙х3² =0 .
Доказать что ΔЕ1Е2Е3 автополярный трёхвершинник.
Достаточность: Найти матрицу Q , используя то, что точка Е1
является полюсом прямой (Е2Е3 ) и т.д. (самостоятельно).
Определение: Четырехвершинник называется вписанным в овальную квадрику, если его вершины инцидентны квадрике.
Теорема. Если четырехвершинник вписан в овальную квадрику, тогда диагональный трехвершинник является автополярным относительно квадрики.
Доказательство. Пусть АВСD – четырёхвершинник вписанный в овальную квадрику и ΔPQR - диагональный трёхвершинник.
Докажем, что Р - полюс прямой (QR).
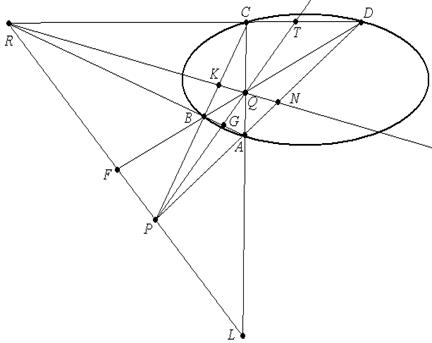
По гармоническим свойствам полного четырехвершинника гармоническими будут: (CB,PK)=(AD,PN)= -1, т.е. точки K и N гармонически сопряжены с точкой Р относительно овальной квадрики, а значит они принадлежат поляре точки Р. В тоже время точки K и N лежат на прямой (QR)  (QR) - поляра точки Р. Для точек Q и R доказательство аналогично. □
(QR) - поляра точки Р. Для точек Q и R доказательство аналогично. □
Замечание: Эта теорема позволяет строить поляру точки если она не инцидентна овальной квадрике.
Дата добавления: 2022-02-05; просмотров: 472;











