Предельные случаи теоремы Паскаля

Рассмотрим овальную квадрику и инцидентный ей шестивершинник А₁ , А₂ , А₃ , А₄ , А₅ , А₆ .

Фиксируем вершину А₁, а вершину А₂ будем перемещать по квадрике так, чтобы она приближалась к точке А₁ , тогда прямая (А₁А₂) будет стремиться к предельному положению - касательной в точке А₁ . Такую фигуру будем называть предельным шестивершинником, он состоит из пяти точек и шести прямых, причем одна точка будет двойная - А₁₂, а прямая (А₁А₂) – касательной.

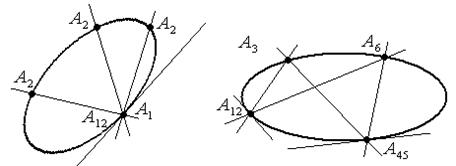
Аналогичным образом могут совпадать вершины какие-либо другие вершины. Например: А₃ = А₄ и/или А₅ =А₆ .

Замечание: Возможны случаи: А₂ = А₃ , А₄ = А₅ , А₆ = А₁ , но не возможно: А₂ = А₄ или А₂ = А₆ , также невозможен случай А₁ = А₂ = А₃ , т.е. совпадать могут только две вершины лежащие на одной стороне.

Определение: Фигура, двойственная шестивершиннику – шестисторонник а₁ а₂ а₃ а₄ а₅ а₆ .

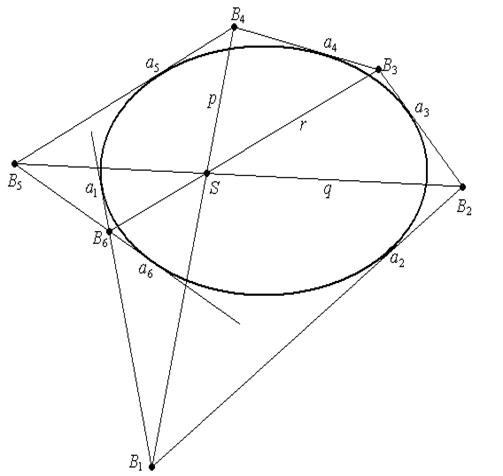
а₁∩а₂=В₁, а₂∩а₃=В₂, а₃∩а₄=В₃ , а₄∩а₅=В₄ , а₅ ∩а₆=В₅ , а₆ ∩а₁=В₆.

Пары вершин - В₁ и В₄ , В₂ и В₅ , В₃ и В₆ называются противоположными.

Теорема Брианшона. Для того чтобы шестисторонник касался овальной квадрики необходимо и достаточно, чтобы прямые, соединяющие противоположные вершины шестисторонника пересекались в одной точке (были инцидентны одной точке).

Замечание: Для этой теоремы тоже существует предельные случаи (рассмотреть самостоятельно.)