Квадрики на проективной плоскости

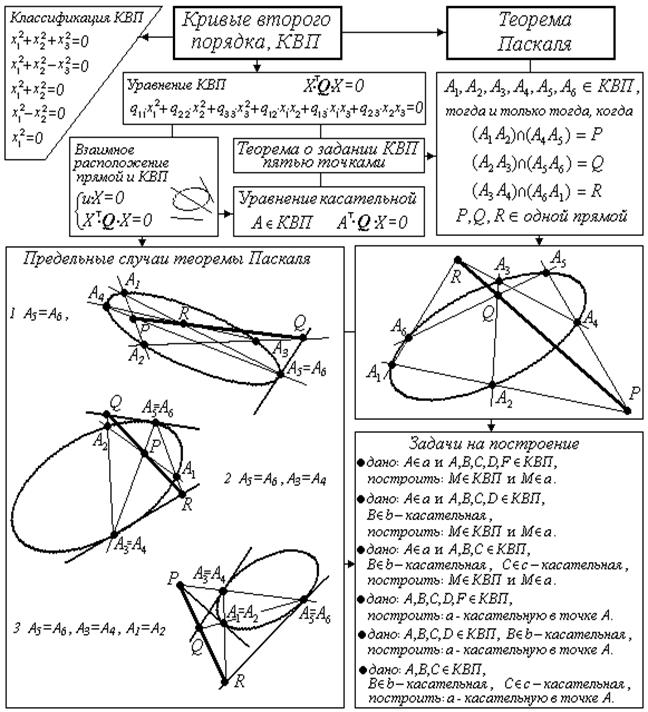
Рассмотрим проективную плоскость над полем действительных чисел (т.е. координаты точек могут быть только действительными числами).

Определение: Множество точек на проективной плоскости Р₂ координаты которых в некотором репере удовлетворяют уравнению 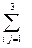q _{i j} ∙х _i ∙х _j = 0 - называется квадрикой или кривой второго порядка (КВП).

В развернутом виде получим: q₁₁∙х₁²+ q₂₂∙х₂² + q₃₃∙х₃²+ 2∙q₁₂∙х₁∙х₂ + 2∙q₁₃∙х₁∙х₃ + 2∙q₂₃∙х₂∙х₃ =0 (*)

Замечание: В силу того, что уравнение квадрики – это однородное уравнение второго порядка, коэффициенты уравнения определяются с точностью до пропорциональности. Т.е. квадрика определена набором из шести чисел с точностью до пропорциональности и среди этих наборов нет нулевого набора ( 0 : 0 : 0 : 0 : 0 : 0 ). (Почему?)

Определение: Матрица Q= 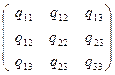-называется матрицей квадрики.

Замечание: МатрицаQ является симметричной, Q=Q^Т .

Уравнение (*) в матричном виде примет вид:

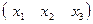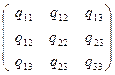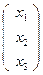∙ ∙ =0 или Х ^Т∙Q∙Х =0 (проверьте).

Свойства квадрик:

1. Ранг матрицы квадрики инвариантен относительно линейного преобразования, задаваемого матрицей А: rangQ = rang(A^T∙Q∙A), так как det A≠0.

2. Преобразованием координат можно привести квадрику к каноническому виду - λ₁∙x₁² + λ₂∙x₂² + λ₃∙x₃² =0, где λ_i - собственные значения матрицы Q.

Замечание: Эти свойства квадрик вытекают из свойств квадратичных форм.

Делая проективное преобразование 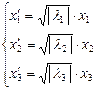, квадрику можно привести к виду:

ε₁∙x₁² + ε₂∙x₂² + ε₃∙x₃² =0, где ε_i = - 1, 0, 1.

Т.е матрица примет вид - 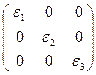и её ранг равен числу ненулевых ε_i.