Деление отрезка в данном отношении

Пусть в пространстве задан произвольный отрезок М₁М₂ и точка М – любая точка этого отрезка, отличная от М₂. Пусть 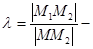число называемое отношением, в котором точка М делит отрезок М₁М_{2. .} Задача о делении отрезка в данном отношении l состоит в том, чтобы по данному отношению и данным координатам точек М₁ и М₂ найти координаты точки М. Решить эту задачу позволяет следующая теорема:

Теорема: Если точка М (х; у; z) делит отрезок М₁М₂ в отношении l, то координаты этой точки определяются по формулам:

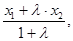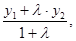Х= у = z =

z

М М ₂

М ₁

у

Х О

Доказательство: По теореме о пропорциональности отрезков (из элементарной геометрии), заключенными между параллельными прямыми, имеем:

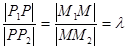, но 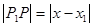, , 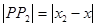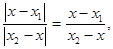т. к. х >х₁ и х₂ > х, имеем х= 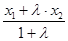. Аналогично доказываются формулы у = 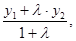z = .

Следствие: Если М₁(х₁; у₁; z₁) и М₂ (х ₂; у ₂; z ₂) – концы отрезка М₁М₂ , а точка М (х; у; z) – середина этого отрезка, то ее координаты находятся по формулам:

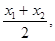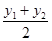Х = у = , z = . (*)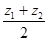

Пример. Даны точки М ₁ (1;1) и М ₂(7;4). Найти точку М (х; у), которая в два раза ближе к М ₁, чем М ₂.

Решение: Искомая точка М делит отрезок М₁М₂ в отношении l =1/2. Применяя формулы (*), находим координаты этой точки: х=3, у=2.