Проекция вектора на ось
Пусть в пространстве заданы ось (прямая с выбранным на ней направлением ) и некоторый вектор  . Проведем через точки А и В плоскости, перпендикулярные оси U. Обозначим через А/ и В/ точки пересечения этих плоскостей с осью
. Проведем через точки А и В плоскости, перпендикулярные оси U. Обозначим через А/ и В/ точки пересечения этих плоскостей с осью
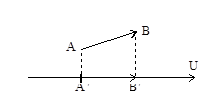

 Определение:Проекцией (геометрической ) вектора
Определение:Проекцией (геометрической ) вектора  на ось U называется вектор А/В/, начало которого А/ – есть проекция начала А на ось U ,а конец В/ - проекция конца В на ту же ось. Обозначается проекция так: Пр u
на ось U называется вектор А/В/, начало которого А/ – есть проекция начала А на ось U ,а конец В/ - проекция конца В на ту же ось. Обозначается проекция так: Пр u  или, короче, Пр
или, короче, Пр  .
.
 Определение: Проекцией (алгебраической) вектора
Определение: Проекцией (алгебраической) вектора  на ось U называется длина вектора А/В/, взятая со знаком «+», если его направление совпадает с направлением оси u и со знаком «–», если их направления противоположны.
на ось U называется длина вектора А/В/, взятая со знаком «+», если его направление совпадает с направлением оси u и со знаком «–», если их направления противоположны.
Обозначение: ПРu  или ПР
или ПР 
Замечание 1:Геометрическая проекция (или компонента) вектора есть вектор, а алгебраическая проекция вектора есть число.
Замечание 2: В задачах, требующих найти проекцию вектора, обычно, имеют в виду алгебраическую проекцию.
Имеет место следующая теорема.
Теорема 1: Проекция вектора  на ось u равна длине вектора
на ось u равна длине вектора  , умноженной на косинус угла между вектором
, умноженной на косинус угла между вектором  и осью u,т. е.ПРu
и осью u,т. е.ПРu =½
=½ ½cos a(1) , где a – угол между вектором
½cos a(1) , где a – угол между вектором  и осью u
и осью u
Доказательство: Если a£ p ¤ 2 (на рисунке под а)), то в силу определения проекции имеем
ПРОХ  = ½ А/ В / ½= ½
= ½ А/ В / ½= ½  ½cos a .
½cos a .
Если же a> p / 2, (см. рис. в)), то в силу вновь определения
проекции имеем ПРОХ  = –½ А/ В / ½= –½
= –½ А/ В / ½= –½  ½cos(p-a)= =½
½cos(p-a)= =½  ½cos a. Таким образом, для любого угла a справедливо данное равенство. g
½cos a. Таким образом, для любого угла a справедливо данное равенство. g
Следствие 1: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой.
Следствие 2: Пусть  =
= 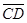 и задана ось l . Тогда справедливо равенство ПРu
и задана ось l . Тогда справедливо равенство ПРu  = ПРu
= ПРu 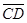 , т.е. равные векторы имеют равные проекции на одну и ту же ось.
, т.е. равные векторы имеют равные проекции на одну и ту же ось.
Дата добавления: 2022-02-05; просмотров: 458;











