Свойства скалярного произведения векторов
Рассмотрим некоторые свойства скалярного произведения векторов:
1. 

 =
= 

 –(коммутмтивность).
–(коммутмтивность).
Доказательство: По определению скалярного произведения

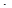
 = ½
= ½  ½
½ 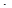 ½
½  ½
½ 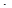 cos j и
cos j и

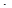
 = ½
= ½  ½
½ 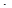 ½
½  ½
½ 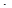 cos j , но ½
cos j , но ½  ½
½ 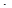 ½
½  ½ = ½
½ = ½  ½
½ 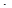 ½
½  ½, поскольку это произведение чисел. Следовательно,
½, поскольку это произведение чисел. Следовательно,


 =
= 

 . g
. g
2. ( l  )
) 
 = l
= l  (
( 

 ) – (ассоциативность)
) – (ассоциативность)
3. 
 (
(  +
+  ) =
) = 

 +
+ 

 – (дистрибутивность).
– (дистрибутивность).
Замечание 1:Данное свойство дает право при скалярном умножении векторных многочленов выполнять действия почленно. В силу свойства 1. можно при этом не заботиться о порядке сомножителей, а свойство 2. позволяет объединить числовые коэффициенты векторных сомножителей, например,
(2  +5
+5  )
)  (3
(3  +4
+4 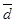 ) = (2
) = (2  +5
+5  )
)  (3
(3  ) + (2
) + (2  + 5
+ 5  )
)  (4
(4 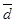 ) = (2
) = (2  )
)  (3
(3  ) +(5
) +(5  )
)  (3
(3  )+(2
)+(2  )
)  (4
(4 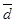 )+ (5
)+ (5  )
)  (4
(4 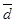 ) =6
) =6 

 + 15
+ 15 

 + 8
+ 8 

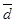 + 20
+ 20 

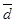 .
.
4. 

 = ½
= ½  ½2
½2
Доказательство: По определению скалярного произведения 

 = ½
= ½  ½
½  ½
½  ½ cos 0 = ½
½ cos 0 = ½  ½2, если ½
½2, если ½  ½¹ 0, т. е. если
½¹ 0, т. е. если  ¹ 0. Если же
¹ 0. Если же  = 0, то также, по определению,
= 0, то также, по определению, 

 = 0. Но в этом случае ½
= 0. Но в этом случае ½  ½= 0 и, значит, равенство
½= 0 и, значит, равенство 

 = ½
= ½  ½2 также справедливо. g
½2 также справедливо. g
Скалярное произведение 

 называется скалярным квадратом вектора
называется скалярным квадратом вектора  и обозначается
и обозначается  2. На основании только что доказанного мы имеем:
2. На основании только что доказанного мы имеем:  2 = ½
2 = ½  ½2 ; отсюда, в частности,
½2 ; отсюда, в частности, 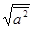 = ½
= ½  ½.
½.
5. Если 

 = 0 и ½
= 0 и ½  ½½
½½  ½¹ 0, то cos j = 0 и j = p/2, т.е. векторы
½¹ 0, то cos j = 0 и j = p/2, т.е. векторы  и
и  перпендикулярны, т.е.
перпендикулярны, т.е. 

 . И обратно, если
. И обратно, если 

 ,то
,то 

 = 0.
= 0.
Замечание 2: Для базисных векторов 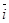 ,
, 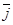 ,
, 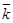 , непосредственно получаем следующие равенства:
, непосредственно получаем следующие равенства: 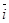 2 =
2 = 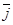 2 =
2 = 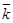 2 =1,
2 =1, 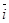

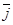 =
= 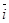

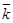 =
= 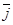

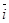 =
= 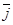

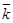 =
= 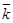

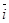 =
= 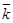

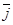 = 0.
= 0.
Дата добавления: 2022-02-05; просмотров: 487;











