Направляющие косинусы вектора
Пусть дан произвольный вектор  ={C;U;Z}; будем считать, что
={C;U;Z}; будем считать, что  выходит из начала координат и не лежит ни в одной координатной плоскости. Проведем через точку М плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед диагональю которого служит отрезок ОМ
выходит из начала координат и не лежит ни в одной координатной плоскости. Проведем через точку М плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед диагональю которого служит отрезок ОМ
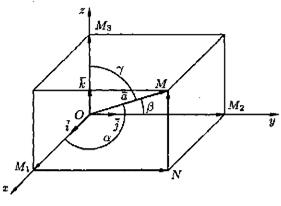
Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,
|ОМ |2 = |ОМ1 |2 + | ОМ2|2 + | ОМ3 |2.
Но |ОМ | =|  |, |
|, | 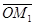 |=|Х|, |
|=|Х|, | 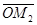 |=|У|, |
|=|У|, | 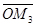 |=|Z |; таким образом, получаем
|=|Z |; таким образом, получаем 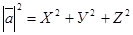 ,
, 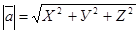 (3).
(3).
Обозначим через α, β, γ углы вектор а  и осями координат. Из формул (1), (2) и (3) получаем
и осями координат. Из формул (1), (2) и (3) получаем
cosα = 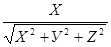 , cos β =
, cos β = 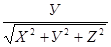 , cos γ =
, cos γ = 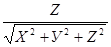 ;
;
cosα, cosβ, cosγ называются направляющими косинусами вектора  .
.
Возводя в квадрат левую и правую части каждого из равенств, и суммируя полученные результаты, имеем:
сos2a + cos 2b +cos2 g = 1, т.е. сумма квадратов направляющих косинусов любого вектора равна единице.
В заключении пункта рассмотрим задачу:
Пусть даны две произвольные точки М1 (х1;у1;z1 ), М2(х2; у2;z2 ). Найдем расстояние d между ними. Используя теорему 2, и формулу (3), сразу получаем искомый результат:
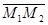 = { х 2 – х; у2 –у 1; z2 –z 1} , а так как d – длина вектора
= { х 2 – х; у2 –у 1; z2 –z 1} , а так как d – длина вектора 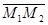 , то d = |
, то d = | 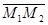 | =
| = 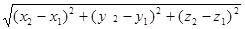 – формула расстояния между двумя точками, заданными своими координатами.
– формула расстояния между двумя точками, заданными своими координатами.
§2 . Разложение вектора по базису
Определение: Пусть задана система координат Охуz в пространстве. Пусть векторы  ,
,  ,
,  – единичные векторы осей координат, т. е. |
– единичные векторы осей координат, т. е. |  | = |
| = |  | = |
| = |  | = 1 (т.е. их длины равны единице; единичные векторы еще называют орт – векторами), и каждый из них одинаково направлен с соответствующей осью координат. Тройка векторов
| = 1 (т.е. их длины равны единице; единичные векторы еще называют орт – векторами), и каждый из них одинаково направлен с соответствующей осью координат. Тройка векторов  ,
,  ,
,  называется базисом.
называется базисом.
Имеет место следующая теорема:
Теорема 3:Любой вектор  может быть единственным образом разложен по базису
может быть единственным образом разложен по базису  ,
,  ,
,  , т. е. представлен в виде:
, т. е. представлен в виде:  = l
= l  +m
+m  + h
+ h  , где l, m, h – некоторые числа.
, где l, m, h – некоторые числа.
Доказательство: Приложив вектор  к началу координат, обозначим его конец через М (смотри рисунок §1, 1,6.). Проведем через точку М плоскости, перпендикулярные осям координат. Пусть М1, М2, М3 – точки пересечения этих плоскостей с осями координат. По определению сложения векторов имеем:
к началу координат, обозначим его конец через М (смотри рисунок §1, 1,6.). Проведем через точку М плоскости, перпендикулярные осям координат. Пусть М1, М2, М3 – точки пересечения этих плоскостей с осями координат. По определению сложения векторов имеем:
 =
= 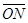 +
+ 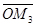 ,
, 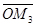 =
= 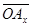 +
+ 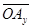 . (1)
. (1)
Из этого равенства получаем  =
= 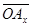 +
+ 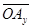 +
+ 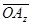 . Так как векторы
. Так как векторы 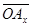 и
и  ,
, 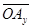 и
и  ,
, 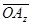 и
и  коллинеарны, то
коллинеарны, то 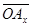 = l
= l  ,
, 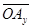 = m
= m  ,
, 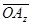 = h
= h  (2), где l, m, h – некоторые числа.
(2), где l, m, h – некоторые числа.
Из равенства (1) и соотношений (2) получаем  = l
= l  +m
+m  + h
+ h  .
.
Для доказательства единственности этого представления установим, что l=Х, m=У , h=Z , где Х, У, Z – координаты вектора  .
.
Покажем, например, что l=Х. Так как Х=½ 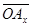 ½, если
½, если 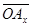 имеет то же направление, что и вектор
имеет то же направление, что и вектор 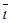 , и Х= - ½
, и Х= - ½ 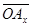 ½, если вектор
½, если вектор 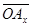 имеет направление, противоположное направлению вектора
имеет направление, противоположное направлению вектора  , то
, то 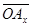 = Х
= Х  . Сравнивая с равенством
. Сравнивая с равенством 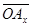 = l
= l  , получаем l = Х. Аналогично показывается, что m = У, h = Z . g
, получаем l = Х. Аналогично показывается, что m = У, h = Z . g
Дата добавления: 2022-02-05; просмотров: 540;











