Mатематическое определение ОС.

Дана функция y = F(x). Введем в неё обратную связь:

y = F(x , y) = F(u), где F(u) - неявная функция.

Это общее математическое определение функций с ОС. Рассмотрим общий случай ОС.

Обратная связь.

Рассмотрим для примера ООС. Выразим её как 2 функции ( 2 процесса ):

x - аргумент сигнала, или прямой связи (прямой передачи),

x₀ – аргумент сигнала обратной связи (ОС, обратной передачи).

Рассмотрим схему:

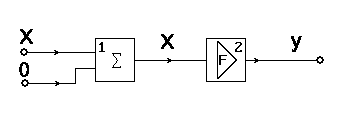
Рис. 1.4.21. Элементы-блоки функции прямой передачи.

В схеме на рис. 1.4.21 ОС отсутствует, здесь показана только функция прямой передачи:

у = F(x) = А (1.4.16),

где А– функция прямой передачи.

Рассмотрим схему, в которую дополнительно включены элементы функции обратной передачи (ОС):

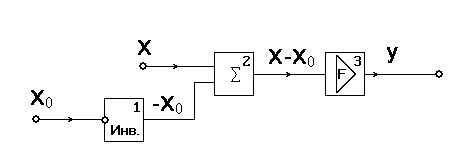
Рис. 1.4.22. Элементы-блоки функции обратной передачи.

Видно, что формула ОС здесь выражается как

y = F(x - x₀ ) (1.4.17)

Из (1.4.17) найдём x:

Теперь вычислим y0 = F(x) , подставив x из выражения (1.4.18):

Выражение (1.4.19) написано для условий, соответствующих как схеме с прямой связью, так и схеме с обратной связью, и для таких условий выделена специально переменная y_0, поскольку значение y₀ может отличаться от решения y в реальной системе с ОС. Осталось выразить y через аргумент ОС х₀ как сложную функцию (см. рис. 1.4.23):

у = H( F(x₀) ) (1.4.20)

Отсюда найдём x₀:

Подставим (1.4.21) в (1.4.19):

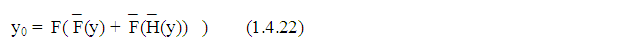
Теперь положим в формуле перехода процессов (см. выше):

Внешняя функция у нас:

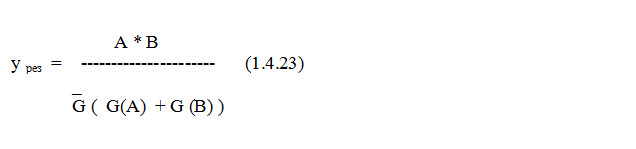
Сравнивая знаменатель (1.4.23) с выражением (1.4.23), мы видим, что в знаменателе мы получили y₀ , поэтому:

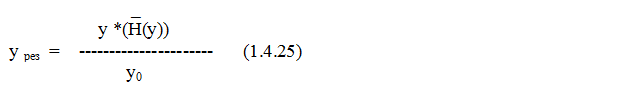
Как видно из (1.4.22), y₀ учитывает как функцию прямой передачи, так и функцию обратной передачи – это было указано в (1.4.19), из-за чего это выражение и было обозначено не как y, а как y₀, то есть величина y₀ несколько парадоксальна и практического значения не имеет, но возможно, что она стремиться к y. Далее находим из выражений (1.4.25), (1.4.16) и (1.4.21) :

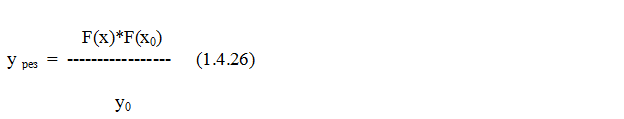
Выражение (1.4.26) представляет собой формулу перехода процессов, которая имеет в своём составе функцию прямой передачи и функцию обратной передачи -y0 сочетает элементы прямой передачи и элементы обратной передачи. Здесь не выведено решение для системы с ОС ( для «чёрного ящика» такого вывода просто нет - решение находится методом подбора с помощью алгоритма ). Здесь показана просто связь системы с ОС с некоторым переходом двух процессов.

Блок-схема нашей системы с ОС показана на рис. 1.4.23.:

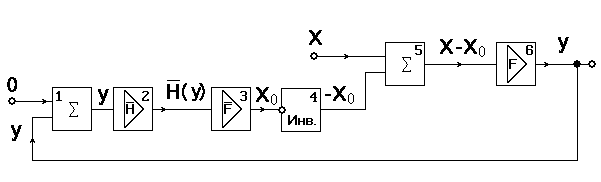
Рис. 1.4.23. Блок-схема системы с ОС: блоки 1 и 5 – сумматоры, блоки 2, 3 и 6 – функциональные усилители, блок 4 – аналоговый инвертор. Блок 6 определяет функцию y = F(x), блоки 2 и 3 определяет функцию:

Математический смысл уравнения (1.4.26) таков: функции прямой передачи и обратной передачи равноправны и являются двумя функциями перехода процессов. Переход процессов имеет внешнюю функцию y =F(x).