Линейные операции над векторами
Векторы. Операции над векторами. Проекция вектора на ось
Основные понятия
Величины, которые полностью определяются своими численными значениями, называются скалярными. Примерами скалярных величин являются: масса, объем, работа, длина, площадь, температура.
Другие величины, например, сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называются векторными.
Определение:Вектором называется направленный отрезок  с началом в точке А и концом в точке В. Если точки А и В совпадают, то вектор называется нулевым и обозначается
с началом в точке А и концом в точке В. Если точки А и В совпадают, то вектор называется нулевым и обозначается 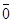 или просто 0. Вектор обозначается так
или просто 0. Вектор обозначается так  или
или  , или выделяется жирным шрифтом а. Направление вектора на рисунке указывается стрелкой
, или выделяется жирным шрифтом а. Направление вектора на рисунке указывается стрелкой


 А В с
А В с
Расстояние между началом и концом вектора называется его длиной или модулем и обозначается: 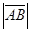 ,
, 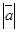 .
.
Определение:Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть направлены одинаково или противоположно.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор будем считать направленным одинаково с любым вектором. Длина его равна нулю, т. е. ½ 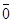 ½=0. Теперь можно сформулировать важное понятие равенства двух векторов.
½=0. Теперь можно сформулировать важное понятие равенства двух векторов.
Определение:Векторы  и
и  называются равными, если они коллинеарны, одинаково направленные и их длины равны.
называются равными, если они коллинеарны, одинаково направленные и их длины равны.
На рисунке изображены слева неравные, а справа - равные векторы  и
и  .
.







Всякие векторы можно «привести к общему началу», т.е. построить векторы, соответственно равные данным и имеющие общее начало в некоторой точке О. Такое приведение показано на рисунке ниже.
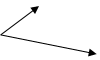


|

 О
О 
В связи с этим векторы называются свободными.
Линейные операции над векторами
Линейными операциями над векторами называются операции сложения, вычитания и умножения вектора на число. Эти действия имеют много общих свойств с алгебраическими действиями, поэтому учение о действиях над векторами называется векторной алгеброй.
 Сложение векторов.
Сложение векторов.
Пусть даны два вектора и
и  . Суммой
. Суммой  +
+  называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора  в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора  . (Правило треугольника.) Графически это выглядит так:
. (Правило треугольника.) Графически это выглядит так: 
Сумму двух векторов можно найти по правилу параллелограмма, для этого вектор  приложите к началу вектора
приложите к началу вектора  , достройте полученную фигуру до параллелограмма. Диагональ, выходящая из начала векторов - есть вектор суммы, т.е.
, достройте полученную фигуру до параллелограмма. Диагональ, выходящая из начала векторов - есть вектор суммы, т.е.  +
+  =
=  .
.

Замечание:Определив сумму двух векторов,можнонайти 
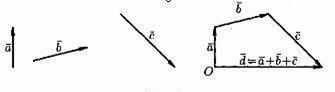
 сумму любого числа данных векторов. Пусть, например, даны три вектора
сумму любого числа данных векторов. Пусть, например, даны три вектора 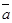 ,
,  ,
,  Сложив
Сложив  и
и  , получим вектор
, получим вектор  +
+  . Прибавив теперь к нему вектор
. Прибавив теперь к нему вектор  , получим вектор
, получим вектор  +
+  +
+ 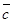 =
= 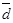
Дата добавления: 2022-02-05; просмотров: 442;











