Арифметичні операції над векторами.
3.2.1. Множення вектора на число.
Означення (множення вектора на число). Множення вектора  на число
на число 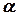 — це операція, результатом якої є вектор, паралельний вектору
— це операція, результатом якої є вектор, паралельний вектору  , співнаправлений вектору
, співнаправлений вектору  , якщо
, якщо 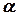 додатне, і протилежно направлений, якщо
додатне, і протилежно направлений, якщо 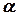 від’ємне, і який має довжину
від’ємне, і який має довжину 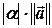 .
.
Отже, множення вектора  на число
на число 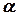 — це розтягування або стискання вектора
— це розтягування або стискання вектора  в
в 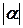 разів (
разів ( 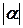 > 1 — розтягування,
> 1 — розтягування, 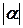 < 1 — стискання) з вибором того ж самого або протилежного напрямків, в залежності від того, додатне
< 1 — стискання) з вибором того ж самого або протилежного напрямків, в залежності від того, додатне 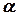 , чи від’ємне.
, чи від’ємне.
3.2.2. Сума двох векторів.
Означення (суми двох векторів за правилом трикутника).Нехай є два вектори  і
і 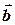 . Перенесемо вектор
. Перенесемо вектор 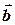 так, щоби його початок співпав з кінцем вектора
так, щоби його початок співпав з кінцем вектора  . Сумою
. Сумою  називається вектор, який сполучає початок вектора
називається вектор, який сполучає початок вектора  з кінцем вектора
з кінцем вектора 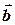 .
.

Означення (суми двох векторів за правилом паралелограма). Нехай є два вектори  і
і 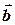 . Перенесемо вектор
. Перенесемо вектор 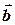 так, щоби його початок співпав з початком вектора
так, щоби його початок співпав з початком вектора  . Добудуємо вектори
. Добудуємо вектори  і
і 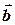 до паралелограму, розглядаючи їх як суміжні сторони, проведемо діагональ паралелограму із спільного початку
до паралелограму, розглядаючи їх як суміжні сторони, проведемо діагональ паралелограму із спільного початку  і
і 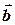 , і зробимо цю діагональ вектором, встановивши його початком спільний початок
, і зробимо цю діагональ вектором, встановивши його початком спільний початок  і
і 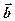 . Утворений таким способом вектор називається сумою
. Утворений таким способом вектор називається сумою  .
.

Теорема (про еквівалентність означень суми векторів). Означення суми векторів за правилом трикутника і за правилом паралелограму еквівалентні, тобто визначають один і той самий результуючий вектор.
Доведення. Довести самостійно, розглянувши відповідний малюнок.
Безпосередньо з означення суми векторів випливає властивість операції додавання векторів, яка називається комутативність:
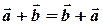
Для доведення розглянемо малюнок:
Тоді 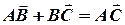 .
.  — паралелограм.
— паралелограм.

Що вийде, якщо сполучити не кінець вектора 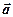 з початком вектора
з початком вектора 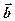 , а навпаки?
, а навпаки?
Нехай 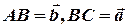 , тоді
, тоді 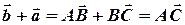 .
.
Виконаємо паралельний перенос вектора 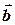 в точку С, тоді
в точку С, тоді  , тоді
, тоді  , так як
, так як  — паралелограм, то
— паралелограм, то 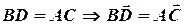 .
.
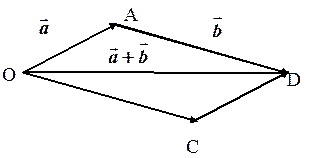
Виконаємо паралельний перенос вектора 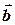 в точку О.
в точку О.
Отримуємо 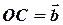 . Виконаємо паралельний перенос вектора
. Виконаємо паралельний перенос вектора 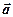 в точку С.
в точку С.
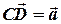 , тоді
, тоді 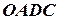 - паралелограм, тобто
- паралелограм, тобто 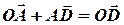 ;
;  .
.
Також безпосередньо з означення суми векторів випливає властивість операції додавання векторів, яка називається асоціативність:
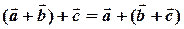
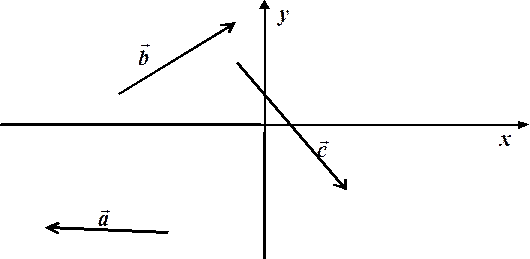
ß
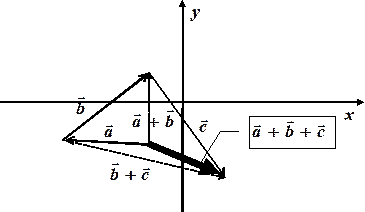
3.2.3. Різниця двох векторів.
У шкільному підручнику з геометрії, як і в багатьох підручниках для вищої школи, означення різниці векторів вводиться, так би мовити, „самостійно” і проголошується, що коли є два вектори, і сполучити їх початки, і утворити вектор з початком у кінці вектора-від’ємника і з кінцем у кінці вектора-зменшуваного, то це і буде, за означенням, різниця даних векторів. Це правильно, але гранично заплутано. Насправді, таке заплутане означення є наслідком класичного означення різниці двох величин:
Означення (різниці двох векторів). Різницею двох векторів  і
і 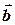 називається такий вектор
називається такий вектор 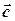 , сума якого з вектором
, сума якого з вектором 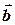 дасть вектор
дасть вектор  .
.
Лема (про різницю векторів).

Доведення. На перший погляд може здатися, що нема чого доводити, але це — тільки на перший погляд. Дійсно, ліва частина формули — це результат операції, визначеної певним чином відповідним означенням. Права частина визначена означеннями операції множення вектора на число і операції додавання векторів. Отже, для доведення формули, треба взяти її праву частину 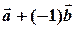 , додати до неї вектор
, додати до неї вектор 
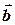 і пересвідчитись, що в результаті буде отримано вектор
і пересвідчитись, що в результаті буде отримано вектор  . Останнє довести самостійно, користуючись означеннями операцій множення вектора на число і додавання векторів.
. Останнє довести самостійно, користуючись означеннями операцій множення вектора на число і додавання векторів.
З означення різниці векторів і з формули  випливає геометричне правило побудови різниці двох векторів: суміщаємо (за допомогою паралельного переносу одного з векторів) початки векторів
випливає геометричне правило побудови різниці двох векторів: суміщаємо (за допомогою паралельного переносу одного з векторів) початки векторів  і
і 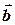 ; з’єднуємо кінці векторів
; з’єднуємо кінці векторів  і
і 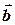 відрізком прямої; перетворюємо відрізок у вектор з напрямком від кінця вектора
відрізком прямої; перетворюємо відрізок у вектор з напрямком від кінця вектора 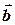 до кінця вектора
до кінця вектора  ; побудований вектор і є різницею векторів
; побудований вектор і є різницею векторів  і
і 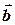 .
.
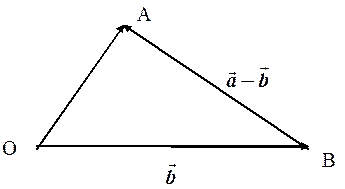
3.2.4. Поняття лінійної комбінації векторів.
У формулюванні властивості асоціативності операції додавання векторів “задіяно” три вектори. Можна уявити ситуацію, коли результуючий вектор визначається будь-якою скінченною сукупністю “твірних” векторів (за приклад можна взяти знаходження результуючої сили у фізиці); при цьому вектори, що беруть участь у такій багатомісній операцій, можуть бути помножені на будь-які дійсні числа. Таким чином виникає поняття лінійної комбінації векторів:
Означення (лінійної комбінації векторів). Нехай задана будь-яка скінченна сукупність векторів

і така сама за кількістю сукупність дійсних чисел
 .
.
Лінійною комбінацією вказаних векторів називається вираз
 .
.
Зауваження. В означенні лінійної комбінації векторів залишився один невизначений момент, а саме: яким має бути порядок виконання операцій додавання? Відповідь: яким завгодно. Це випливає з властивості асоціативності операції додавання векторів (зрозуміло, що спочатку, у будь-якому порядку, ми множимо вектори на відповідні числа, а потім, у будь-якому порядку, сумуємо отримані вектори).
Дата добавления: 2021-05-28; просмотров: 764;











