Формула повної ймовірності

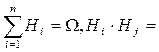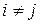На практиці зустрічаються ситуації, коли деяка подія А може відбутися тільки разом з однією з подій Н₁, Н₂, ..., Н_п, які утворюють повну групу подій ( Æ, ). Якщо ймовірності подій Н₁, Н₂, ..., Н_п позначити 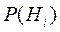>0 (і=1,2, ...,п), то ймовірність події А обчислюється за формулою

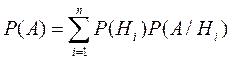, (6)

яка називається формулою повної ймовірності. Випадкові події Н₁, Н₂, ..., Н_п називаються гіпотезами.

Задача 16. Досліджуються результати екзамену з теорії ймовірностей у двох групах. У першій групі з 28 студентів 10 отримали оцінку „відмінно”, а в другій – з 22 студентів 7 студентів отримали оцінку „відмінно”. Яка ймовірність того, що навмання вибраний студент отримав на екзамені оцінку „відмінно”?

Розв’язання. Випробування – навмання обираємо одного студента із двох груп. Подія А – навмання вибраний студент на екзамені отримав оцінку „відмінно”. Це може статися, якщо студента вибрали з першої групи (гіпотеза Н₁), або з другої (гіпотеза Н₂). За статистичним означенням ймовірності маємо:

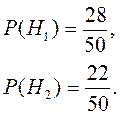
Схематично задача 16 представлена на рис. 3.

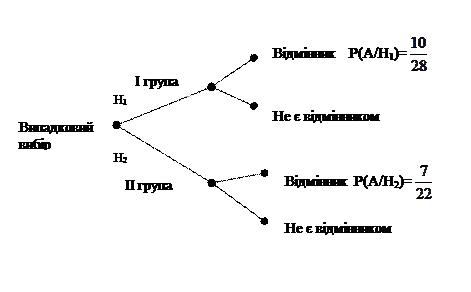
Рис. 3.

Застосуємо формулу повної ймовірності у випадку двох гіпотез

.

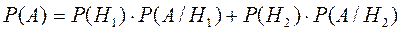Підставивши числові значення, маємо

.

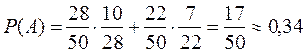Відповідь: 0,34.

Формула Бейєса

Нехай виконуються ті ж умови, що й для формули (6).

Для переоцінки ймовірностей гіпотез Н_і (і=1,2, ...,п ) за умови, що подія А здійснилася ( 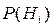>0), тобто для обчислення ймовірностей 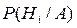і=1,2, ...,п, користуються формулою Бейєса:

= .

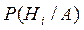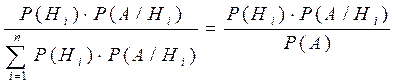Отже, формула Бейєса дає відповідь на запитання: якщо подія А здійснилася, то яка ймовірність того, що вона здійснилася з Н_і гіпотезою.

Задача 17. У першому ящику маємо 8 стандартних і 2 браковані деталі, а у другому – 5 стандартних і 5 бракованих. Ящики ідентичні. З навмання обраного ящика навмання взято дві деталі, які виявилися стандартними. Яка ймовірність того, що їх взяли з другого ящика?

Розв’язання Випробування – з навмання обраного ящика навмання взято дві деталі. Введемо позначення: подія А – взято дві стандартні деталі; гіпотеза Н₁ – навмання взяті дві стандартні деталі з першого ящика; гіпотеза Н₂ – навмання взяті дві стандартні деталі з другого ящика.

Обчислимо ймовірності цих подій

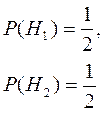
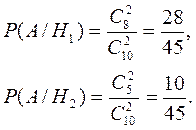
Для переоцінки ймовірності Н₂ використаємо формулу Бейєса:

.

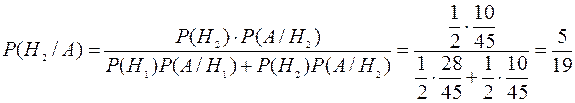Відповідь: .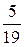

Запитання для самоконтролю

1. Що називають повною групою подій?

2. Записати формулу повної ймовірності.

3. Які події називаються залежними? Навести приклад.

4. Дати означення умовної ймовірності. Навести приклад.

5. Записати формулу Бейєса. Які умови її використання?