Теорема множення ймовірностей залежних подій

Якщо події А і В залежні, то ймовірність добутку цих подій дорівнює добутку ймовірностей однієї з них на умовну ймовірність іншої, за умови, що перша подія відбулася, тобто

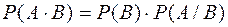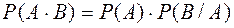або (2)

Наслідок . Ймовірність добутку скінченої кількості залежних подій обчислюється за формулою

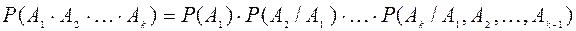
Задача 13. Студент прийшов на екзамен, знаючи лише 20 з 25 екзаменаційних питань. Яка ймовірність того, що він знає відповіді на всі три запитання?

Розв’язання Випробування – студент отримає три запитання.

подія А₁ – студент знає відповідь на перше запитання;

подія А₂ – студент знає відповідь на друге запитання;

подія А ₃ –студент знає відповідь на третє запитання.

Оскільки студент знає відповіді лише на 20 запитань із 25, то події А₁, А₂, А₃ – залежні. Тому для розв’язання задачі скористаємося формулою (2) для випадку трьох залежних подій

.

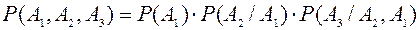Маємо .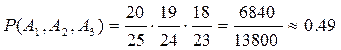

Відповідь: 0,49.

Зауваження. Теореми множення ймовірностей використовуються для того, щоб дати відповідь на запитання: „Події, що розглядаються, залежні чи ні?”

У випадку залежності подій спрацьовує формула (2), у випадку незалежних подій – формула (1).

Приклад. З колоди 36 карт навмання виймають одну карту. Припустимо здійснення таких подій:

подія А – взята карта пікова;

подія В – взята карта дама.

Визначимо залежні події чи ні? Для цього розглянемо добуток подій А і В – подію АВ: „взята карта пікова дама”.

Знайдемо ймовірність подій А, В та АВ:

Р(А)= 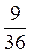; Р(В)= 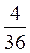; Р(АВ)= .

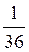Відповідно до зауваження, якщо події А і В незалежні, то справедливою буде рівність 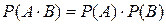, а якщо залежні, то ця рівність не виконуватиметься. Перевіряємо її, підставляючи значення ймовірностей,

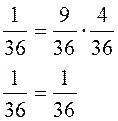
Рівність справедлива, отже події А і В – незалежні.