Теорема додавання ймовірностей несумісних подій
Якщо події А і В несумісні (АВ=Æ), то ймовірність суми цих подій дорівнює сумі їх ймовірностей
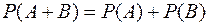 (3)
(3)
Наслідок 1. Ймовірність суми скінченої кількості попарно несумісних подій дорівнює сумі ймовірностей цих подій
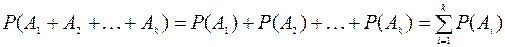 .
.
Наслідок 2. Ймовірність протилежної до А, події 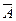 дорівнює
дорівнює 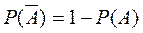
Наслідок 3. Сума ймовірностей подій, що утворюють повну групу, дорівнює одиниці 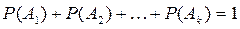 .
.
Задача 14. У ящику 10 червоних і 6 синіх ґудзиків. Навмання виймають два ґудзики. Яка ймовірність того, що ґудзики будуть одного кольору?
Розв’язання. Випробування – витягування з ящика двох ґудзиків. Подія А – ґудзики одного кольору; подія А1 – ґудзики червоні; подія А 2 – ґудзики сині.
Очевидно А=А1+А2, і події А1 і А2 несумісні. Скористаємося формулою (3) 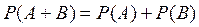 . Спочатку обчислимо Р(А1) та Р(А2).
. Спочатку обчислимо Р(А1) та Р(А2).
Число способів взяти 2 ґудзики з 16 дорівнює 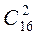 . Число випадків, сприятливих для події А1 дорівнює
. Число випадків, сприятливих для події А1 дорівнює 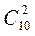 , сприятливих для події А2 –
, сприятливих для події А2 – 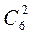 .
.
Одержимо, 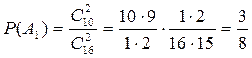 ;
;
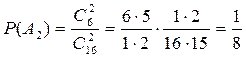 .
.
Отже, 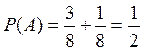 .
.
Відповідь. 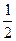 .
.
Теорема додавання ймовірностей сумісних подій.
Якщо події А і В сумісні, то ймовірність суми цих подій дорівнює сумі їх ймовірностей без ймовірності їх добутку
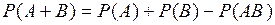 (4)
(4)
Зауваження 1. Якщо події А та В незалежні, то формула (4) набуває вигляду: 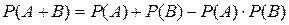 .
.
Зауваження 2. Якщо події А та В залежні, то формула (4) набуває вигляду: 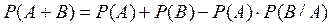
або
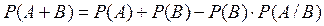 .
.
Дата добавления: 2022-02-05; просмотров: 457;











