Ймовірність відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях

Нехай k – число настання події А в п незалежних випробуваннях, в кожному з яких подія А може відбутися з ймовірністю р (0<р<1) , 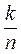– відносна частота події А.

З інтегральної теореми Муавра – Лапласа випливає

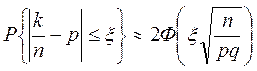(11)

Задача 22. Ймовірність настання події в кожному з 10000 незалежних випробувань дорівнює 0,75. Знайти ймовірність того, що відносна частота настання події відрізняється від ймовірності за абсолютною величиною не більше ніж на 0,001.

Розв’язання. За умовою п=10000, 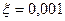, р=0,75, q=0,25.

Підставивши у формулу (11) числові значення, отримаємо:

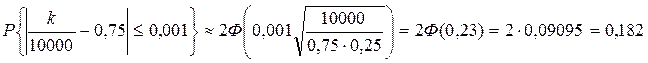Відповідь:0,182.

Задача 23. Скільки разів потрібно кинути монету, щоб з ймовірністю 0,6 можна було сподіватися, що відхилення відносної частоти появи герба від ймовірності р=0,5 буде за абсолютною величиною не більше 0,01?

Розв’язання. За умовою 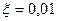, р=0,5, q=0,5.

Застосувавши формулу (11), отримаємо:

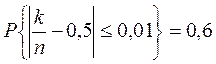. Очевидно, що

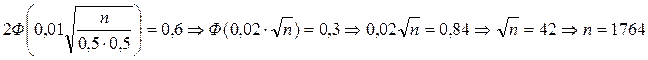Відповідь:1764 рази.

Запитання для самоконтролю

1. Записати формулу Бернуллі.

2. Записати формулу найімовірнішого числа настання випадкової події.

3. Записати формулу Пуассона. При яких умовах вона застосовується?

4. Сформулювати локальну та інтегральну теореми Муавра-Лапласа.

5.Чому дорівнює ймовірність відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях?

Практичні заняття