Пусковые моменты несимметричных двухфазных микромашин

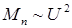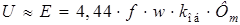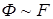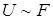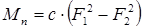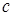Известно, что пусковые моменты асинхронных и синхронных двигателей Известно, что пусковые моменты асинхронных и синхронных двигателей при асинхронном пуске пропорциональны квадрату фазного напряжения, т.е. . Поскольку , то при отсутствии насыщения магнитной цепи , следовательно, , где – коэффициент пропорциональности.

.

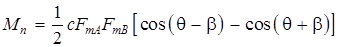Подставляя (1.5), (1.6) в последнее равенство, получим:

С учетом того, что

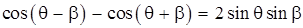
окончательно будем иметь:

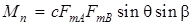(2.4)

Следовательно, пусковой момент несимметричного двухфазного двигателя пропорционален произведению амплитуд намагничивающих сил и синусам углов их пространственного и временного сдвигов. Важно отметить, что максимум момента будет пр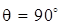и и .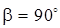

2.3. Метод симметричных составляющих применительно
к несимметричным двухфазным микромашинам

Для исследования несимметричных двухфазных микромашин могут использоваться различные методы.

1. Метод двух реакций. Суть метода заключается в том, что намагничивающие силы, поля и потокосцепления обмоток статора и ротора раскладываются по двум взаимно перпендикулярным осям. Метод особенно эффективен при анализе явнополюсных синхронных микромашин с неравномерным воздушным зазором.

2. Метод вращающихся полей. Он основан на представлении любой m – фазной машины суммой m однофазных машин, в каждой из которых имеются прямо и обратно вращающиеся поля.

3. Метод симметричных составляющих. По существу сводится к тому, что двухфазная несимметричная система токов или НС раскладывается на две симметричные системы: прямую и обратную, каждая из которых создает свое круговое магнитное поле, вращающееся в прямом или обратном направлении. Метод получил наибольшее признание в трудах Ю. С. Чечета и его учеников Ф. М. Юферова, Е. М. Лопухиной и др.

Подавляющее большинство современных микромашин переменного тока имеют на статоре две обмотки, сдвинутые в пространстве на 90 эл. градусов, что продиктовано стремлением получить максимальное круговое поле при минимальных токах в обмотках. Вместе с тем, редко удается сдвинуть токи в обмотках на угол, равный 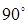во времени. Поэтому на практике чаще приходится иметь дело с несимметричными временными системами токов, намагничивающих сил, магнитных потоков и т.д.

Согласно методу симметричных составляющих любую систему двух векторов 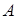и 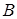разных по величине, сдвинутых во времени на произвольный угол, можно разложить на две симметричные составляющие системы равных по величине векторов и сдвинутых во времени на .

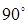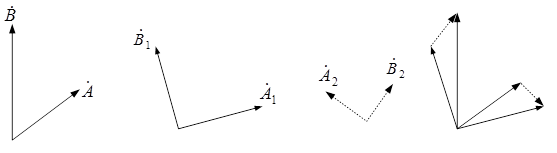
а б в г

Рис. 2.3. Несимметричная система векторов (а) и ее симметричные
составляющие (б, в, г).

Одна из симметричных систем имеет порядок чередования векторов, совпадающий с исходной, и называется прямой последовательностью, другая имеет обратный порядок чередования векторов и называется обратной последовательностью (рис. 2.3).

Выразим заданные векторы 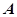и 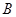через симметричные составляющие

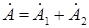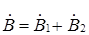; (2.5)

Как видно из рис. 1.4, симметричные составляющие связаны между собой соотношением:

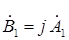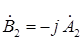, (2.6)

Подставляя (2.6) в (2.5) и решая уравнения с двумя неизвестными, получим выражения симметричных составляющих через векторы исходной системы [1]:

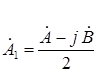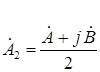; . (2.7)

На рис. 2.4 выполнено графическое разложение несимметричной системы векторов 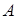и Bна симметричные составляющие с использованием уравнений (2.6) и (2.7).

На практике при анализе двухфазных микромашин в качестве векторов A и Bиспользуют векторы НС 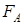и 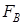, потоков 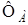и 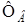, токов 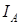и 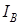и т. д.

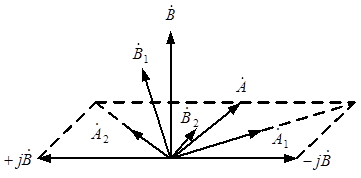
Рис. 2.4. Графическое разложение несимметричной системы векторов
на симметричные составляющие

Метод симметричных составляющих пригоден не только для анализа несимметричных двухфазных микромашин, но и как предельный случай несимметрии – однофазных микромашин, полагая, что ток и его симметричные составляющие в одной из обмоток, которой фактически нет, равен нулю.

Задача 2.2. Разложить графически несимметричные системы векторов на симметричные составляющие.

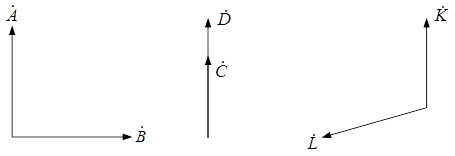
а б в