Главные оси и главные моменты инерции

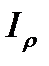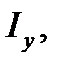Представим себе плоскую фигуру, моменты инерции которой относительно осей координат и а полярный момент инерции относительно начала координат 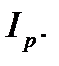Как было установлено ранее,

.

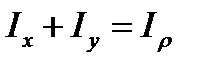Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты инерции будут изменяться, причем

.

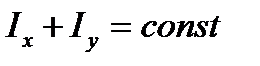Если сумма двух переменных величин остается постоянной, то одна из них уменьшается, а другая увеличивается. Следовательно, при каком-то положении осей один из осевых моментов достигает максимального значения, а другой - минимального значения.

Оси, относительно которых моменты инерции имеют максимальное и минимальное значения, называются главными осями инерции.

Момент инерции относительно главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, то она называется главной центральной ось, а момент инерции относительно этой оси - главным центральным моментом инерции.

Особо важным является то обстоятельство, что если фигура имеет ось симметрии, то эта ось всегда будет одной из главных центральных осей.

Введем еще одну геометрическую характеристику плоского сечения.

Центробежным моментом инерции плоской фигуры называется взятая по всей площади фигуры сумма произведений элементарных площадок на произведение расстояний этих площадок до двух данных взаимно перпендикулярных осей:

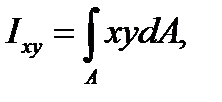(3.15)

где х, у - расстояние от площадки dA до осей у и х. Центробежный момент инерции может быть положительным, отрицательным и в частном случае равным нулю.

Если взаимно перпендикулярные оси х и у, или одна из них являются осью симметрии плоской фигуры, то относительно таких осей центробежный момент инерции равен нулю.

Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений.

КРУЧЕНИЕ