Главные оси и главные моменты инерции.

Определим угол α₀,на который нужно повернуть оси произвольной системы координат, чтобы осевые моменты инерции имели экстремальные значения.

Найдем производную, 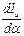и приравняем ее к нулю: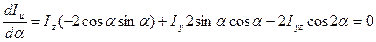

откуда,

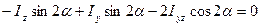
Объединим слагаемые последнего выражения при множителе 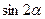и заменим угол α углом α₀ ,тогда получим:

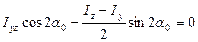(8.28)

Согласно выражению (8.27), левая часть зависимости (8.28) есть центробежный момент инерции относительно главных центральных осей рассматриваемого сечения. Следовательно, центробежный момент инерции относительно главных осей инерции равняется нулю.

Зависимость (8.28) является условием для нахождения положения главных осей инерции. Из этого условия находим:

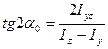(8.29)

Если α₀>0, то для нахождения положения главных осей инерции необходимо оси произвольной системы координат повернуть на угол α₀ против часовой стрелки.

Если α₀ <0, то для нахождения положения главных осей инерции необходимо оси произвольной системы координат повернуть на угол α₀ в направлении движением часовой стрелки.

Если поперечное сечение бруса имеет ось симметрии, то эта ось является одной из главных осей инерции. Вторая ось главной системы осей инерции расположена перпендикулярно к первой.

Величины главных моментов инерции определяются по формулам (8.25) и (8.26) при замене угла α углом α₀. Эти формулы можем привести к более удобному для практического использования виду, если выразить тригонометрические функции через моменты инерции сечения относительно произвольных осей координат. Используем следующие соотношения, известные из тригонометрии:

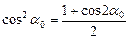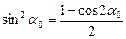, ,тогда формулы (8.25) и (8.26) принимают вид:

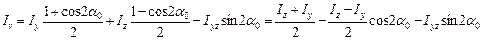
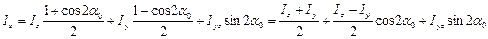
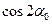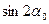Выразим и в последних зависимостях, через 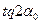, а затем 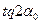выразим последних выражениях, нерции относительно главных центральных осей рассматриваемого сечениячерез осевые моменты и центробежный момент инерции сечения относительно первоначально выбранных осей координат, в результате получим:

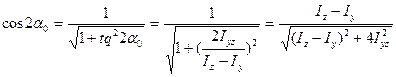
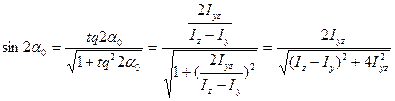
В результате подстановки этих выражений в формулы (8.25) и (8.26) главных моментов инерции сечения, получаем:

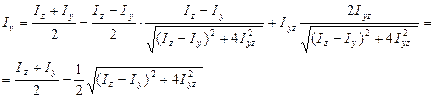
Аналогично

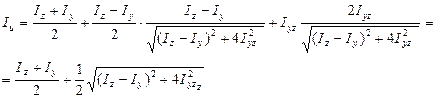
Последние две формулы можно объединить и записать в следующем виде:

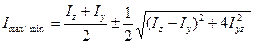(8.30)

При определении максимального значения момента инерции принимается верхний знак плюс, а при определении минимального значения момента инерции принимается нижний знак минус.

Если I_z >I_y, то I_uбудет иметь максимальное значение, а ось uбудет осью максимальной инерции. ПриI_z < I_y ось vбудет осью максимальной инерции.