В нашей задаче моменты сопротивления следующие

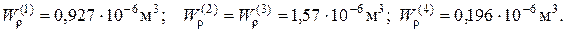
По ним вычислим величины крутящих моментов начала образования пластических деформаций каждого участка:

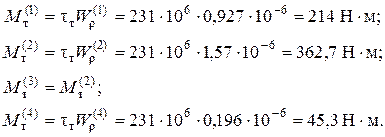
Приравняв эти моменты текучести сечений к моментам, полученным в результате статического расчёта (рис.2,г), найдём тот участок, на котором появится текучесть и величину внешнего крутящего момента:

214 = 0,8 М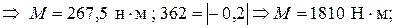

362 = 0,8 М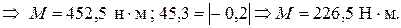

Таким образом, видим , что наименьший внешний момент, от которого возникнет пластичность в вале, будет равен М_т = 226,5 н ∙ м, причём

пластические деформации при этой величине момента появятся на четвёртом участке. При увеличении М (М > 226,5 Н∙м) пластичность на четвёртом участке будет развиваться вглубь, к центру сечения, а при

М = 267,5 н ∙ м пластические деформации появятся на первом участке.

2.2. Определение предельных моментов сечений. Зависимость касательных напряжений от сдвиговых деформаций определяется диаграммой сдвига (рис.3), поэтому эпюра касательных напряжений в поперечном сечении (рис.4) – это диаграмма сдвига, взятая до величины γ_мах. Момент в сечении вычислим как сумму моментов от касательных напряжений, вычисленных в упругой зоне (площадь F _уп ) пластической зоне (площадь F_пл) (рис.4):

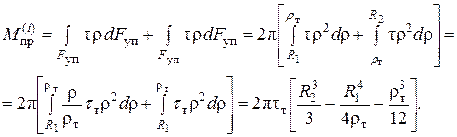
Для первого участка ρ_т = R₁ , тогда

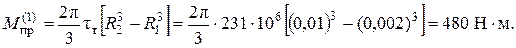
Для остальных участков R₁ = 0, тогда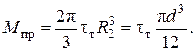

Теперь

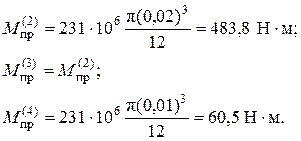
Напомним, что это внутренние характеристики сечений - при та­ких значениях моментов всё сечение будет находиться в состоянии пластичности (рис.5).

Приравняем внутренние предельные моменты сечений к моментам упругого расчёта (рис.2,г):

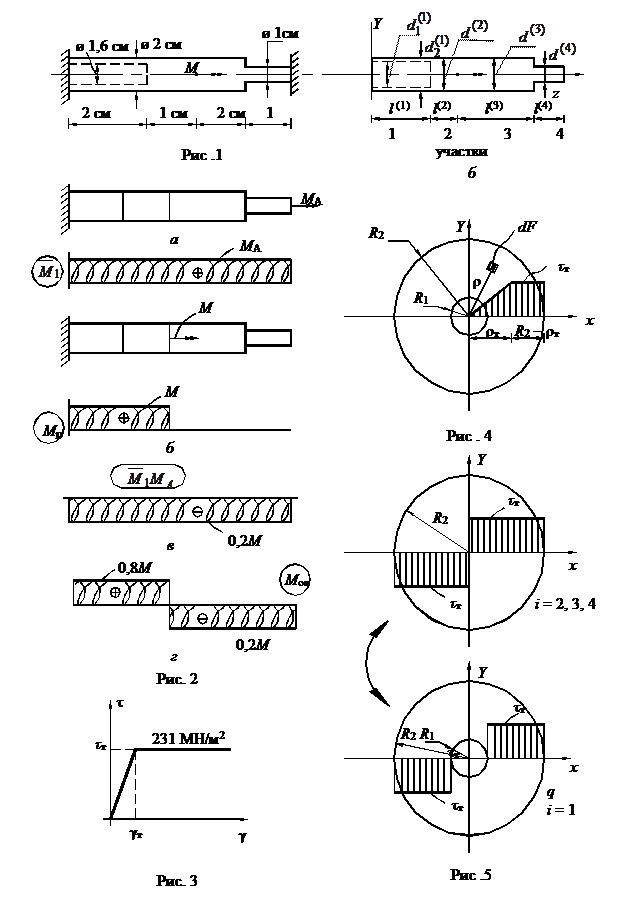
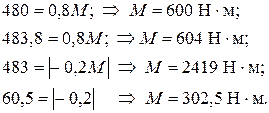
Отсюда получим величину предельного грузового момента. При нагрузке

М = 302,5 Н·м четвертый участок будет полностью нахо­диться в состоянии пластического деформирования .При дальней­шем увеличении М

(М > 302,5) крутящий момент на четвёртом уча­стке, согласно диаграмме (рис.3), увеличиваться не будет - он всегда будет равен 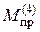= 60,5 Н·м, а статически неопределимый вал теперь можно рассматривать как статически определимую конструкцию. Процесс развития зон пластичности в сечениях вала изобразим на рис.6.

2.3 Определим предельный внешний момент. Известно, что первый

участок имеет предельный момент 480 Н·м. Поэтому предельную на­грузку для всей конструкции (т.е. нагрузку, при достижении которой вал не в состоянии сопротивляться нагрузке) найдём из уравнения равновесия (рис.6,г):

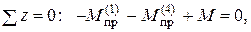или – 480 – 60,5 + М = 0,

отсюда М _пр = М = 540,5 Н·м - более высокую нагрузку ваг выдержать не сможет.