Схемы замещения несимметричных двухфазных микромашин
Примем за базовую микромашину машину с двумя обмотками на статоре A и B, сдвинутыми в пространстве на угол 90 эл. градусов. Обмотки питаются от сети несимметричных переменных напряжений 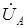 и
и 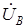 . В цепь обмотки B включен конденсатор C. Ротор – короткозамкнутый (рис. 3.1,а).
. В цепь обмотки B включен конденсатор C. Ротор – короткозамкнутый (рис. 3.1,а).
Напряжения 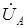 и
и 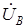 можно представить как сумму падений напряжений
можно представить как сумму падений напряжений 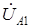 ,
, 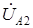 и
и 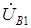 ,
,  от токов прямой и обратной последовательностей на сопротивлениях
от токов прямой и обратной последовательностей на сопротивлениях 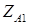 и
и 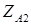 ,
, 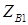 и
и 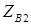 :
:
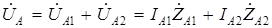 ;
;
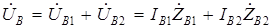 . (3.1)
. (3.1)
Важно отметить, что в общем случае векторы напряжений 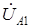 ,
, 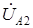 и
и 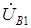 ,
,  не образуют двух симметричных систем напряжений. На симметричные составляющие раскладываются лишь векторы токов, а сопротивления фаз различны из–за наличия конденсатора в фазе
не образуют двух симметричных систем напряжений. На симметричные составляющие раскладываются лишь векторы токов, а сопротивления фаз различны из–за наличия конденсатора в фазе 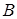 .
.
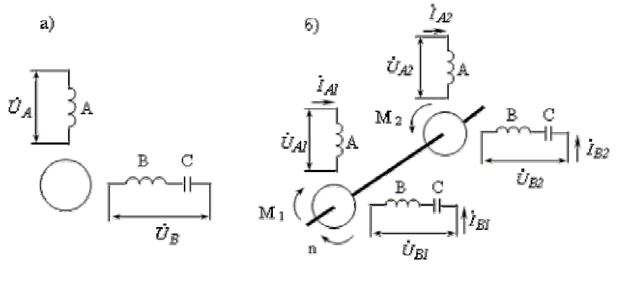
Рис. 3.1. Схема базовой машины (а) и ее физическая модель (б).
Токи прямой и обратной последовательностей создают круговые вращающиеся магнитные поля. Поэтому машину на рис. 3.1, а можно заменить физической моделью, состоящей из двух симметричных машин, расположенных на одном валу и развивающих встречно–направленные моменты (рис. 3.1, б). Поскольку прямое поле больше обратного, "прямая" машина мощнее "обратной", поэтому общий вал вращается в прямом направлении со скоростью 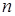 . При этом ротор прямой машины вращается по полю – она работает в режиме асинхронного двигателя. Скольжение ротора
. При этом ротор прямой машины вращается по полю – она работает в режиме асинхронного двигателя. Скольжение ротора 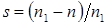 . Ротор обратной машины вращается встречно обратному полю – она работает в режиме электромагнитного тормоза. Скольжение ротора относительно этого поля будет
. Ротор обратной машины вращается встречно обратному полю – она работает в режиме электромагнитного тормоза. Скольжение ротора относительно этого поля будет
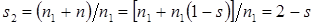 .
.
В соответствие с физической моделью базовой машины для несимметричного двухфазного микродвигателя можно построить 4 схемы замещения: две для токов прямой и обратной последовательностей фазы A, две для токов прямой и обратной последовательностей фазы B. Эти схемы представлены на рис. 3.2
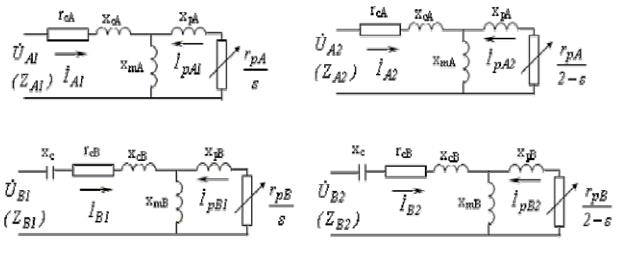
Рис. 3.2. Схемы замещения несимметричной двухфазной машины
В схемах замещения:
rcA, rcB, xcA, xcB – активные и реактивные сопротивления обмоток статора соответственно фаз A и B;
rpA, rpB, xpA, xpB – приведенные к статору (соответственно к числу витков фаз 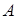 и
и 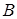 ) активные и реактивные сопротивления ротора;
) активные и реактивные сопротивления ротора;
xmA, xmB – индуктивные сопротивления взаимоиндукции между статором и ротором соответственно фаз 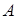 и
и 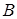 ;
;
xc – реактивное сопротивление конденсатора.
Приведенные на рис. 3.2 схемы замещения в контуре намагничивания не содержат активных сопротивлений, с помощью которых учитываются потери в стали. Это намного упрощает математический анализ и выражения ряда величин, получаемых из схем замещения. Учет же потерь в стали микромашин производится иначе (см. далее).
Схемы замещения, приведенные на рис. 3.2, можно преобразовать, заменив параллельное соединение сопротивлений на последовательное (рис. 3.3).
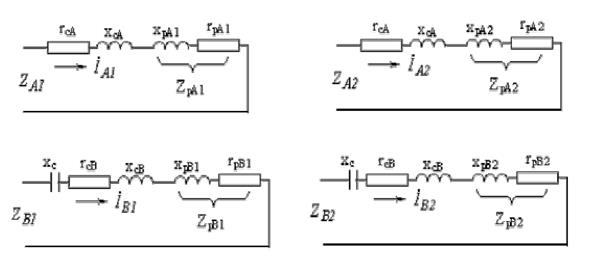
Рис. 3.3. Преобразованные схемы замещения несимметричной двухфазной машины
Здесь (для фазы А):
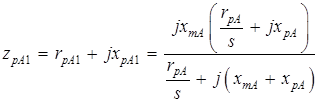 ;
;
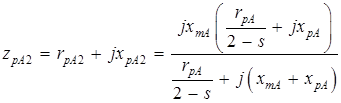 . (3.1)
. (3.1)
Умножив числители и знаменатели этих выражений на сопряженные комплексы соответствующих знаменателей и разделив действительные и мнимые части комплексов, после преобразований получим выражения активных и реактивных сопротивлений параллельных ветвей:
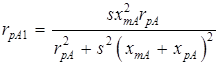 ;
; 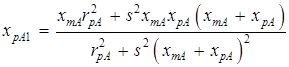 ;
;
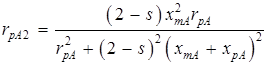 ;
;
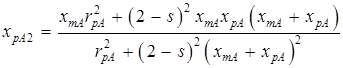 . (3.2)
. (3.2)
Выражения сопротивлений фазы 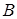 будут иметь аналогичный вид с разницей лишь в индексах.
будут иметь аналогичный вид с разницей лишь в индексах.
Если сложить соответственно активные и реактивные сопротивления преобразованных схем замещения, получим весьма простые схемы.
Однако эта простота обманчива, ибо все сопротивления в схемах замещения рис. 3.4 являются переменными, зависящими от скольжения 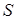 .
.
Полные их значения равны:
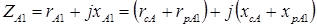 , (3.3)
, (3.3)
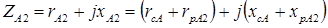 , (3.4)
, (3.4)
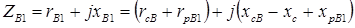 , (3.5)
, (3.5)
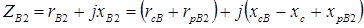 . (3.6)
. (3.6)
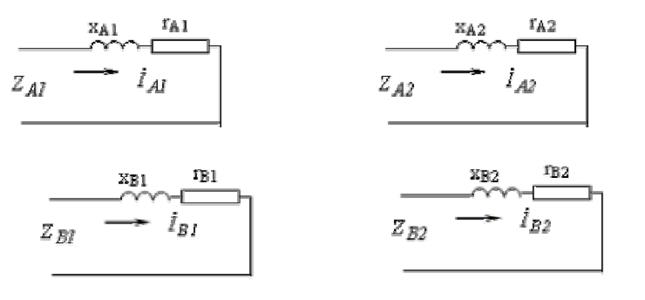
Рис. 3.4. Окончательные схемы замещения несимметричных двухфазных
микромашин
Параметры схемы замещения фазы 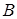 можно выразить через параметры фазы
можно выразить через параметры фазы 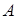 . Если обмотки
. Если обмотки 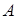 и
и 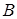 занимают равное число одинаковых по форме пазов статора
занимают равное число одинаковых по форме пазов статора 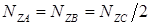 :
:
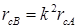 ;
; 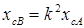 ;
; 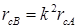 ;
; 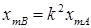 ;
; 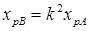 ;
; 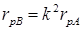 , (3.7)
, (3.7)
где 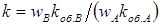 – коэффициент трансформации двигателя.
– коэффициент трансформации двигателя.
Часто в двухфазных двигателях обмотки 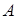 и
и 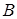 занимают неодинаковое число пазов статора. Так, в двигателях с пусковым элементами рабочая обмотка укладывается в 2/3 пазов статора
занимают неодинаковое число пазов статора. Так, в двигателях с пусковым элементами рабочая обмотка укладывается в 2/3 пазов статора 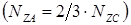 , а пусковая – в
, а пусковая – в 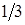 пазов
пазов 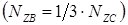 . В этом случае [1]:
. В этом случае [1]:
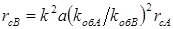 ;
; 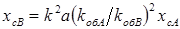 , (3.8)
, (3.8)
где 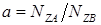 , – соотношение числа пазов, занимаемых обмотками статора;
, – соотношение числа пазов, занимаемых обмотками статора; 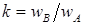 – коэффициент трансформации, равный отношению числа физических витков обмотки
– коэффициент трансформации, равный отношению числа физических витков обмотки 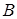 к числу физических витков обмотки
к числу физических витков обмотки 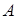 .
.
Параметры ротора и контура намагничивания выражаются, как и в первом случае.
Задача. При каком условии сопротивление схемы замещения 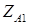 будет равно сопротивлению схемы замещения
будет равно сопротивлению схемы замещения 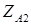 , а
, а 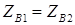 ?
?
Уравнения токов
Повторим еще раз уравнения (2.8):
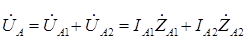 ;
;
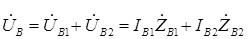
Согласно методу симметричных составляющих
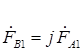 или
или 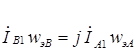 ;
;
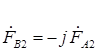 или
или 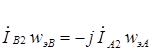 ,
,
где 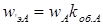 ,
, 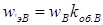 – эффективные числа витков фаз
– эффективные числа витков фаз 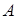 и
и 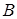 .
.
Разделив левую и правую части последних выражений на wэB, получим
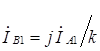 ;
; 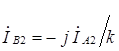 , (4.1)
, (4.1)
где 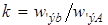 – уже известный коэффициент трансформации двигателя.
– уже известный коэффициент трансформации двигателя.
Подставляя (4.1) в выражение 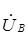 и решая систему двух уравнений относительно
и решая систему двух уравнений относительно 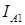 ,
, 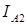 получим
получим
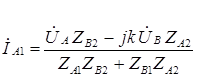 ,
, 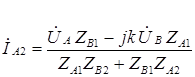 . (4.2)
. (4.2)
Рассчитав 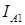 и
и 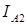 , легко определить
, легко определить 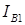 и
и 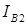 , а затем найти полные токи фаз
, а затем найти полные токи фаз 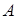 и
и 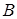 .
.
Дата добавления: 2022-02-05; просмотров: 425;











