Частота вращения эллиптического поля

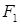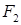На рис. 2.1 показаны векторы прямо и обратно вращающихся НС ( или ), а также вектор результирующей НС 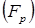в различные моменты времени. Из рисунка видно, что большая ось эллипса равна удвоенной сумме, а малая ось удвоенной разности намагничивающих сил 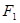и :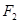

.

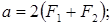
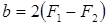Из последнего выражения легко увидеть, что при равенстве нулю одной из НС ( 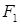или 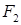), поле становится круговым, а при равенстве НС друг другу ( 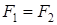) оно превращается в пульсирующее, т.е. эллипс вырождается в линию.

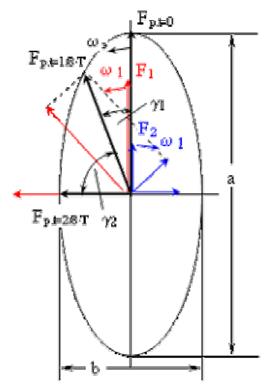
Рис. 2.1. К вопросу о частоте вращения эллиптического поля

Будем фиксировать через каждые 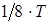прямо и обратно вращающиеся НС 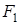, 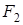и их сумму 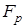. За одно и то же время векторы 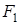и 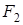каждый раз будут поворачиваться на углы 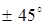, а их сумма 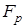первый раз повернется на угол 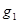, второй раз на угол 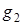и т. д. Из рис. 1.2 видно, что 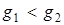, а поскольку временные отрезки одинаковые, это означает, что 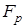вращается с переменной частотой.

Следовательно, эллиптическое магнитное поле вращается с переменной угловой частотой: большей возле малой оси эллипса и меньшей возле большой оси эллипса.

Исследованиями установлено [1], что

, (2.1)

где: 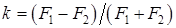– коэффициент формы эллипса.

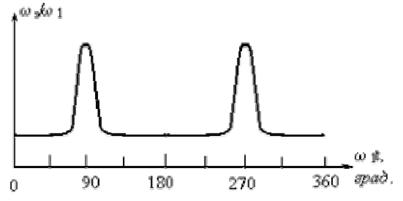
Рис. 2.2. Осциллограмма мгновенной скорости эллиптического поля.

Используя формулу (2.1), найдем максимальные и минимальные значения мгновенной скорости вращения эллиптического поля.

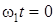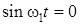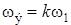Если , то , , , а поскольку коэффициент 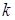меньше 1, . Если , то , , 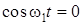, 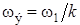а поскольку коэффициент 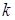меньше 1, .

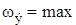На рис. 2.2 показана осциллограмма мгновенной скорости вращения эллиптического поля.

Эллиптическое поле вызывает неодинаковое насыщение участков магнитной цепи (где поле больше, там и насыщение больше), неодинаковые потери в стали, неодинаковые нагревы этих участков, магнитострикционные шумы.

Задача 2.1. Определите во сколько раз 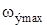и 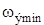отличаются от синхронной 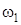, если ?

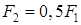2.1. Получение кругового вращающегося магнитного поля
в несимметричных двухфазных микромашинах

Эллиптическое магнитное поле станет круговым, если одна из составляющих, например 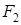,будет равна 0:

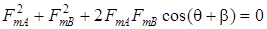(2.2)

Формула (2.2) справедлива, если:

1.

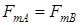
2. .

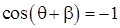Отсюда вытекают два условия получения кругового магнитного поля в несимметричных двухфазных микромашинах:

1. амплитуды намагничивающих сил должны быть равны по величине, т.е.

2. сумма углов их пространственного и временного сдвига должна быть равна 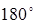, т.е. .

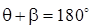Так как 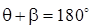, то в формуле (1.5) 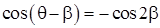или 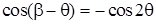. Тогда величина круговой НС будет

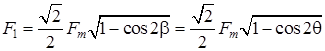(2.3)

Анализ формулы (1.9) показывает, что магнитное поле хотя и круговое, но не максимальное, если углы 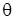и 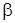каждый в отдельности не равен .

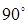Задача 2.1. Определить, во сколько раз величина круговой НС при 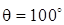и отличается от значения при .