Неполные уравнения плоскости
В общем уравнении полагаем:
1). D = 0 Ax + By + Cz = 0 , плоскость проходит через начало координат .
z
x 0 y
2). A = 0 By + Cz + D = 0 , плоскость параллельна оси ox.
z
o y
x
A =D =0 By +Cz =0 , плоскость проходит через ось ox.
z
o y z
x
3). В = 0 Аx +Cz +D = 0 , плоскость параллельна оси оy. o y
40 x
B =D = 0 Ax + Cz = 0 , плоскость проходит через ось оy.
z
o y
x
4). C = 0 Ax + By + D = 0 , плоскость параллельна оси oz.
z
x o y
C = D =0 Ax + By = 0 , плоскость проходит через ось oz.
z
o y
x
5). А = В =0 Сz + D = 0 , плоскость параллельна координатной плоскости XOY.
z
o y
x
6). A =C = 0 By + D = 0 , плоскость параллельна координатной плоскости XOZ.
z
o y
x
7). B = C = 0 Ax + D = 0, плоскость параллельна координатной плоскости YOZ.
z
o
y
x
8). A =B = D = 0 Cz = 0 или z = 0 , координатная плоскость XOY.
z
o y
x
9). B =C = D = 0 Ax = 0 или x = 0 , координатная плоскость YOZ.
z
o z
x y
10). А = С = D = 0 By = 0 или y = 0 , координатная плоскость XOZ. o y
x
Пример.Найти уравнение плоскости , проходящей через ось OX и точку М(1,2,3).
Решение.Уравнение плоскости имеет вид By + Cz = 0 ; найдём В и С. Подставим координаты точки в это уравнение 2В + 3С = 0 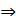 В =
В = 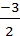 С подставляем в уравнение
С подставляем в уравнение 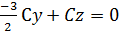 , сокращаем на С, окончательно
, сокращаем на С, окончательно 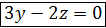
Дата добавления: 2016-06-05; просмотров: 2415;











