Расстояние от точки до плоскости

Задача.Найти расстояние от точки 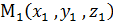до плоскости Q: Ax+By+Cz+D=0.

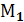. (x₁ ,y₁ ,z₁)

d

Q

Решение.Воспользуемся формулой , которую применим без доказательства:

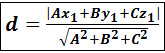→формула расстояния от точки до плоскости.

Пример.Найти расстояние от точки 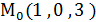до плоскости 3x+4y+5z+3=0.

Решение.d = 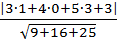= 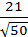. Ответ.d =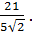

Прямая в пространстве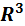

Линию в пространстве рассматривают , как множество всех точек , принадлежащих двум пересекающимся поверхностям 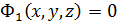и

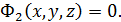
Например: 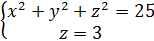при пересечении сферы и плоскости получаем

окружность. Прямую линию получим при пересечении двух плоскостей.

Общее уравнение прямой в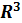

Это уравнение , заданное пересечением двух плоскостей :

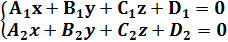→общее уравнение прямой.

Пример. Построить прямую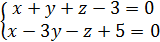

Решение.Чтобы построить прямую, надо задать две точки, для этого найдём точки пересечения прямой с координатными плоскостями.

1). Z =0, 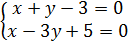решаем эту систему, находим точку пересечения .

2) . X = 0 ,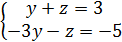

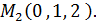
Определение.Точка пересечения прямой с координатной плоскостью называется следомпрямой.

Z .М₂

o .М₁ y

x

Векторное уравнение прямой . Параметрические