Полярная система координат
Полярная система координат состоит из начала точки О, называемой полюсоми лучом ОМ , соединяющем полюс с произвольной точкой М плоскости .
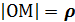 - полярный радиус – вектор точки, угол
- полярный радиус – вектор точки, угол 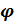 , образованный лучом ОМ и полярной осью - полярный угол точки. (рис.1). Угол
, образованный лучом ОМ и полярной осью - полярный угол точки. (рис.1). Угол 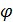 считается положительным при отсчёте от полярной оси против часовой стрелки.
считается положительным при отсчёте от полярной оси против часовой стрелки.
Если точка М имеет полярные координаты 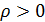 и
и 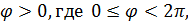 то ей же отвечает и бесчисленное множество пар полярных координат (
то ей же отвечает и бесчисленное множество пар полярных координат ( 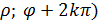 и [-
и [- 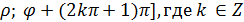
. M y
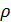 y .M (
y .M ( 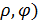
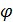
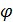
o  o x x=
o x x= 
рис. 1 рис.2
Если начало декартовой прямоугольной системы координат совместить с
полюсом , а ось Оx направить по полярной оси (рис.2) , то прямоугольные координаты x и y точки М и её полярные координаты 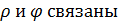 следующими формулами :
следующими формулами :
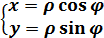 (1)
(1) 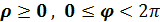 ,
, 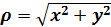 ,
, 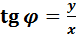 .(2)
.(2)
Пример1.Построить точки в полярной системе координат (п.с.к.): 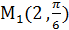 ,
, 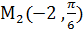 ,
, 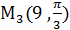 .
.
Решение.0 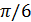
 . M3
. M3
. М1 OM3=9
 ОМ1 =2 .М2 ОМ2 =-2
ОМ1 =2 .М2 ОМ2 =-2 
0  0
0 
Пример 2. Записать уравнение линии в декартовой системе координат (д.с.к.):
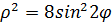
Решение. Из формулы (1) находим 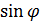 =
=  , подставляем в уравнение кривой , а также из формулы (2) подставляем
, подставляем в уравнение кривой , а также из формулы (2) подставляем 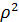 , получаем
, получаем 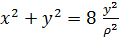 = 8
= 8 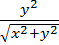 .
.
Возведём в квадрат обе части последнего равенства и приходим к уравнению
( 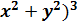 = 64
= 64 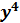 .
.
Пример 3. Записать уравнение линии в п. с. к. ( 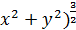 = 4 (
= 4 ( 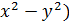
Решение.Из формул (1) вместо x и y подставляем значения , получим
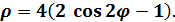
Пример 4.В полярной системе координат построить кривую 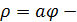 спираль Архимеда, приняв
спираль Архимеда, приняв 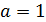 .
.
0 
Домашнее задание.
Построить линии в полярной системе координат
1). 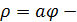 спираль Архимеда.
спираль Архимеда.
2). 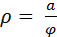 - гиперболическая спираль.
- гиперболическая спираль.
3). 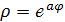 - логарифмическая спираль.4).
- логарифмическая спираль.4). 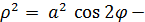 лемниската Бернулли. 50
лемниската Бернулли. 50
5). 
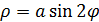 - четырёхлепестковые розы.
- четырёхлепестковые розы.
6). 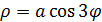
 - трёхлепестковые розы.
- трёхлепестковые розы.
7).  кардиоида.
кардиоида.
8). 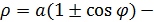 кардиоида.
кардиоида.
Лекция 13. Кривые второго порядка
Определение. Кривой второго порядка называется линия , определяемая уравнением второй степени A 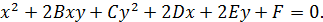
1). Окружность – геометрическое место точек равноудалённых от одной точки , называемой центром.
Каноническое уравнение окружности ( 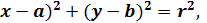 C(
C( 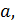 b )-центр окружности , r – радиус окружности
b )-центр окружности , r – радиус окружности
Пример.Привести уравнение окружности 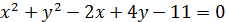 к каноническому виду.
к каноническому виду.
Решение.Выделяем полные квадраты при переменных 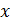 и
и 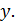
( 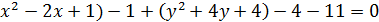
 (
( 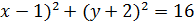
Ответ. ( 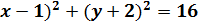 , C (1,-2) r = 4.
, C (1,-2) r = 4.
2). Эллипс.
Определение. Эллипсомназывается множество точек плоскости , сумма расстояний каждой из которых от 2-х данных точек этой плоскости , называемых фокусами , есть величина постоянная ( при условии , что эта величина больше расстояния между фокусами).
y.М(x,y)М 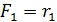 ; M
; M 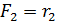 ;
; 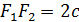 ;
;
r1 r2 M 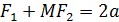 ; M
; M 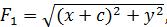
F1 0 F2 x M 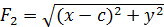 . M
. M 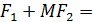
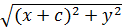 +
+ 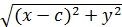 = 2
= 2 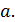
F1 (-c,0) ; F2 (c;0). После освобождения от корней и , про-
ведя некоторые преобразования , получим каноническое уравнение эллипса
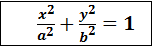 , где
, где 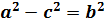
y
B Точки пересечения с осями: x = 0 ,y 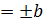 , y = 0,
, y = 0,
x = 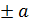 . A
. A 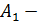 большая ось. B
большая ось. B 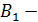 малая ось.
малая ось.
A a . 0 A1 x Определение.Отношение 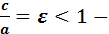 экс -
экс -
В В1 51
центриситет эллипса. 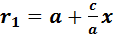 ,
, 
Пример.Построить эллипс 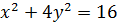 , найти
, найти  и фокусы.
и фокусы.
Решение.Уравнение запишем в виде 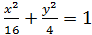 ,
, 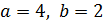 , c=
, c= 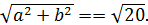
 Чтобы построить эллипс , на осях координат отложим 2
Чтобы построить эллипс , на осях координат отложим 2 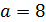 по оси оx , 2b = 4 по оси оy, построим прямоугольник со сторонами 8 и 4 и в него впишем эллипс. y
по оси оx , 2b = 4 по оси оy, построим прямоугольник со сторонами 8 и 4 и в него впишем эллипс. y
4 4 x
3). Гипербола.
Определение.Гипербола– это геометрическое место точек абсолютная величина разности расстояний каждой из которых от 2-х данных точек, называемых фокусами есть величина постоянная ( при условии , что эта величина не равна нулю и меньше расстояния между фокусами).
y .M(x,y) 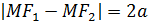
 M
M 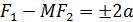
r1 r2 Проделав преобразования , получим каноничес-
F1(-c,0)F2(c,0)x коеуравнение гиперболы: 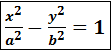 , где
, где
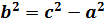 ;2b – мнимаяось; 2
;2b – мнимаяось; 2 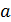 – действитель-
– действитель-
наяось. 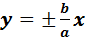 - асимптоты гиперболы ;
- асимптоты гиперболы ;
b 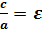
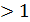 – эксцентриситет гиперболы . Гипербо-
– эксцентриситет гиперболы . Гипербо-
a a ла симметрична относительно оси оx и оy.
b Для построения гиперболы на оси оx отложим 2 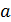 ,
,
на оси оy 2b , строим прямоугольник с этими сто-
ронами , проводим в нём диагонали – это асимптоты гиперболы . Гипербола называется равнобочной , если 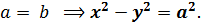 Две гиперболы
Две гиперболы 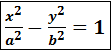 и
и 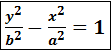 называются
называются
сопряжёнными . Фокальные радиусы 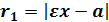 ,
, 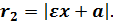
4).Парабола .
Определение.Парабола – множество точек , равноудалённых от данной точки , называемой фокусом и данной прямой , называемой директрисой(фокус не лежит на директрисе).
y Уравнение директрисы : 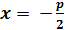 .MN = MF.
.MN = MF.
. M(x,y) F( 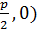 , MN = QM + QN =
, MN = QM + QN = 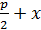 ,
,
 , приравняем
, приравняем
 , возведём в квадрат
, возведём в квадрат
y 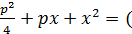
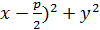 или
или
x= 
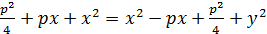 , получим
, получим
0F( 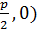 x
x 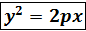 – каноническоеуравнение
– каноническоеуравнение
 параболы.
параболы.
Если уравнение параболы имеет вид , 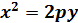 ,
,
то парабола симметрична относительно оси оy, а уравнение директрисы y = -  .y
.y
0 x
Пример.Дана парабола y2 = 6x . Составить уравнение её директрисы и найти её фокус.
Решение. 2p = 6 ; p = 3 , x= - 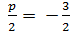 →уравнение директрисы. F(
→уравнение директрисы. F( 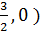 →фокус.
→фокус.
Дата добавления: 2016-06-05; просмотров: 3436;











