Координатная форма смешанного произведения
Пусть вектор 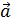 = { X1 , Y1 Z1 } ; вектор
= { X1 , Y1 Z1 } ; вектор 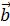 = { X2 ,Y2 ,Z2 } ; вектор
= { X2 ,Y2 ,Z2 } ; вектор  = {X3 ,Y3 , Z3 }.
= {X3 ,Y3 , Z3 }.
[ 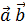 ] =
] = 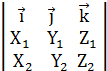 =
= 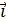
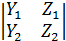 -
- 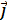
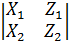 +
+ 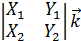 . Известно , что скалярное произведение - это произведение одноимённых координат , поэтому
. Известно , что скалярное произведение - это произведение одноимённых координат , поэтому
( 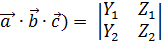 X3 -
X3 - 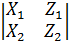 Y3 +
Y3 + 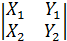 Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки.
Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки.
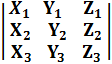 = (
= ( 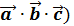 (
( 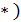
Используя формулу (  , можно доказать все свойства (1,2,3) смешанного произведения.
, можно доказать все свойства (1,2,3) смешанного произведения.
Пример.Вычислить объём пирамиды с вершинами в точках : О ( 0,0,0) ; А(5,2,0) ; В ( 2, 5, 0) ; С ( 1,2,4) .
Решение.Объём пирамиды равен  объёма параллелепипеда , то есть = Vпир. =
объёма параллелепипеда , то есть = Vпир. = 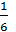 Vпар. =
Vпар. = 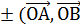 ,
, 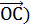 =
= 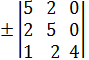 =
= 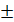 (100 -16 ) = 84 куб.ед.
(100 -16 ) = 84 куб.ед.
Ответ:Vпир.= 84 куб. ед.
Условие компланарности векторов
Теорема.Необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения.
Доказательство необходимости. Пусть 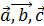 компланарны , значит построить параллелепипед на них нельзя , то есть объём равен нулю V=0 , а это значит и
компланарны , значит построить параллелепипед на них нельзя , то есть объём равен нулю V=0 , а это значит и 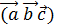 =0 ч.т.д.
=0 ч.т.д.
Доказательство достаточности.Пусть ( 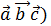 = 0 это значит , что V=0 и векторы
= 0 это значит , что V=0 и векторы 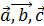 лежат в одной плоскости , то есть компланарны ч.т.д.
лежат в одной плоскости , то есть компланарны ч.т.д.
Вывод:Условием компланарности векторов является равенство нулю их смешанного произведения 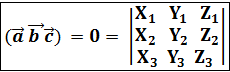 = 0
= 0
Пример.Проверить лежат ли четыре точки в одной плоскости. А ( 2,-1,1); В(5,5,4); С(3,2,-1) ; Д(4,1,3).
Решение. Надо проверить лежат ли 3 вектора 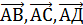 в одной плоскости, для этого найдём координаты этих векторов
в одной плоскости, для этого найдём координаты этих векторов 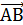 {3,6,3} ;
{3,6,3} ; 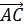 { 1,3,-2} ;
{ 1,3,-2} ; 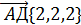
( 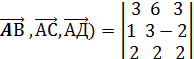 =18 -24 +6 -18-12+ 12= 18
=18 -24 +6 -18-12+ 12= 18  . Вывод.Эти точки
. Вывод.Эти точки
не лежат в одной плоскости.
Определение.Двойным векторным произведением векторов 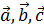 называется векторное произведение [
называется векторное произведение [ 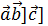 или [
или [ 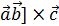 .
.
Задачи
Задача 1. Какому условию должны удовлетворять векторы 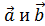 , чтобы вектор
, чтобы вектор 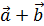 делил пополам угол между векторами
делил пополам угол между векторами 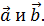
Задача 2.Точка 0 является центром тяжести треугольника АВС. Доказать , что
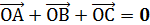 .
.
Задача 3. Найти сумму и разность векторов 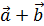 и
и 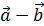 , если
, если 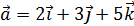 ;
; 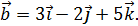
Задача 4.Дан вектор 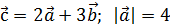 ;
; 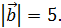 Угол
Угол 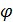 между векторами
между векторами 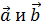 равен 600 . Найти
равен 600 . Найти 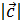 =?
=?
Задача 5.Даны 3 вектора 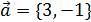 ,
, 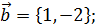
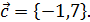 Определить разложение вектора
Определить разложение вектора 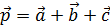 по базису
по базису 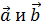 .
.
Дата добавления: 2016-06-05; просмотров: 2826;











