Уравнение плоскости в отрезках
Рассмотрим общее уравнение плоскости Ax + By + Cz + D = 0. Перенесём D вправо и разделим на D: 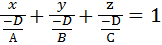 , обозначим
, обозначим 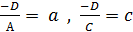
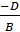 = b, уравнение примет вид:
= b, уравнение примет вид: 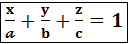
 уравнение плоскости в
уравнение плоскости в
отрезках, где a, b , c отрезки , которые плоскость отсекает от осей координат.
Пример. Построить плоскость 2 x + 5 y – 10 = 0. Приведём это уравнение к уравнению в отрезках 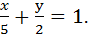 На оси ox отложим отрезок x = 5, на оси oy отложим отрезок y = 2. z
На оси ox отложим отрезок x = 5, на оси oy отложим отрезок y = 2. z
o 2 y
x 5
Лекция 11. Угол между плоскостями . Условия параллельности и перпендикулярности плоскостей.
 Плоскости заданы общими уравнениями.
Плоскости заданы общими уравнениями. 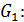
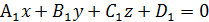 и
и
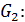
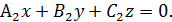
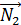
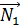
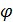
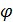
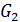

 =
= 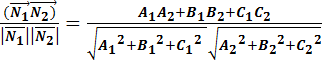
1). Если 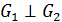 , то (
, то (  или в координатах
или в координатах
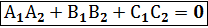 →условие перпендикулярности плоскостей.
→условие перпендикулярности плоскостей.
2). Если 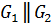 , то
, то  в координатах
в координатах 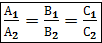 →условие параллельности плоскостей.
→условие параллельности плоскостей.
Пример 1.Составить уравнение плоскости , проходящей через точку 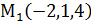 параллельно плоскости 3x + 2y – 7z +8 = 0.
параллельно плоскости 3x + 2y – 7z +8 = 0.
Решение.3(x+2y) + 2(y-1) – 7(z-4) = 0. 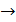 Ответ. 3x + 2y - 7z +14 = 0
Ответ. 3x + 2y - 7z +14 = 0
Пример 2. Через точку 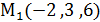 провести плоскость , перпендикулярную плоскостям
провести плоскость , перпендикулярную плоскостям 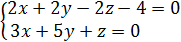
Решение. Уравнение плоскости находим по формуле уравнения плоскости , проходящей через точку , то есть А(x + 2) + B(y – 3) + C (z – 6)=0. Из рисунка вид-
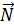 но , что нормальный вектор иско-
но , что нормальный вектор иско-
мой плоскости перпендикулярен
нормальным векторам данных
плоскостей . 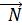 ⊥
⊥ 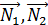 , поэтому
, поэтому
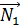
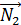
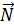 =
= 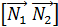 =
= 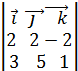 = 13
= 13 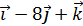 .
.
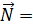 { 13 , -8 , 1 } .Ответ.
{ 13 , -8 , 1 } .Ответ. 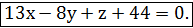
Дата добавления: 2016-06-05; просмотров: 3101;











