Через координаты перемножаемых векторов
Пусть вектор 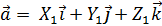 а вектор
а вектор 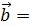
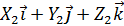 , найдём их скалярное произведение (
, найдём их скалярное произведение ( 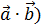 =
= 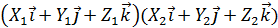 =
= 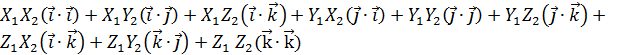 = { (
= { ( 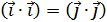 =
= 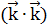 =1, другие ска-
=1, другие ска-
лярные произведения базисных векторов равны нулю, так как они взаимно перпендикулярны } = 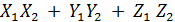 .
.
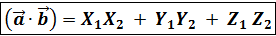
Запишем основные формулы в декартовых координатах :
п 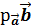 =
= 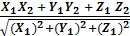 ;
; 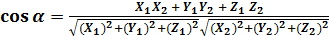 ;
;
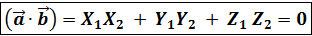 → условие перпендикулярности 2-х векторов.
→ условие перпендикулярности 2-х векторов.
Пример. Найти работу силы 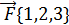 по перемещению в направлении вектора
по перемещению в направлении вектора 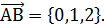
Решение.А = ( 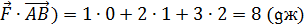 .
.
Векторное произведение векторов
Правые и левые тройки векторов
Определение.Тройка векторов 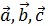 называется правой ( левой ) , если после приведения к одному началу , вектор
называется правой ( левой ) , если после приведения к одному началу , вектор  располагается по ту сторону плоскости , определяемой векторами
располагается по ту сторону плоскости , определяемой векторами 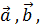 откуда поворот от
откуда поворот от 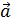 к
к 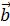 свершается против часовой стрелки ( по часовой стрелки).
свершается против часовой стрелки ( по часовой стрелки).


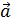
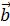
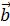
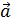
Левая Правая
Определение. Аффинная система координат называется правой ( левой ) , если три базисных вектора образуют правую ( левую ) тройку.
Определение. Векторным произведением вектора 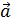 на вектор
на вектор 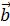 называется вектор
называется вектор  , который удовлетворяет 3- м условиям:
, который удовлетворяет 3- м условиям:
1). 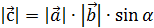 ;
;
2). Вектор 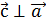 и
и 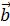 ;
;
 3). Вектор
3). Вектор  направлен так , что образует правую тройку с векторами
направлен так , что образует правую тройку с векторами 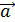 и
и 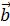 ;
;
Обозначается 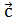
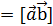 или
или 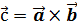 .
.
Дата добавления: 2016-06-05; просмотров: 3022;











