Понятие линейной зависимости векторов

Определение.Линейной комбинацией n векторов 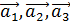….. 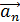называют сумму произведений этих векторов на произвольные вещественные числа , то есть выражение вида :

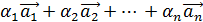, (1)

где 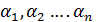- числа.

Определение. Векторы 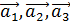….. 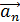называются линейно зависимыми , если найдутся такие числа 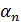, из которых хотя бы одно не равно нулю , что линейная комбинация (1) обращается в ноль 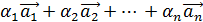= 0.

Определение. Векторы 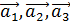….. 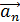называются линейно независимыми , если равенство нулю их линейной комбинации (1) возможно лишь в случае , когда все 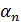= 0.

Теорема 1. Необходимым и достаточным условием линейной зависимости 2-х векторов является их коллинеарность.

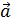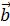Доказательство необходимости.Пусть 2 вектора и зависимы , докажем , что они коллинеарны.

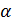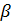По определению линейной зависимости векторов найдутся такие и , что 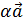+ 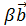=0, пусть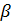 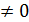,тогда разделим на 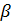, получим +

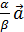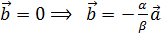
Последнее равенство означает , что векторы коллинеарны ч.т.д.

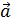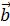Доказательство достаточности.Пусть и коллинеарны , то есть 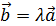или 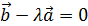это значит зависимы ,ч.т.д.

Теорема 2. Необходимым и достаточным условием линейной зависимости 3-х векторов является их компланарность.

Теорема 3. Любые 4-е вектора в 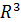линейно зависимы.