ЛЕКЦИЯ 6. Длина вектора. Направляющие косинусы.
Пусть вектор 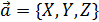 , так как он является диагональю параллелограмма , то по теореме из школы
, так как он является диагональю параллелограмма , то по теореме из школы 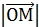 2 =
2 = 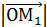 2 =
2 = 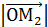 2 =
2 = 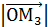 2 или
2 или 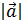 2 = X2 +Y2 +Z2 отсюда
2 = X2 +Y2 +Z2 отсюда
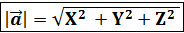 (1)
(1)
Рассмотрим вектор 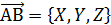 ; точки А(
; точки А( 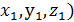 и В (
и В ( 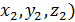
z A
B 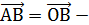
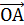 ;
; 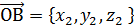 ;
; 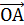 ={
={ 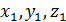 } ,
} ,
k так как 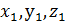 и
и 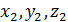 - проекции , то
- проекции , то
x i j y 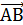 = {
= { 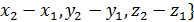 , a модуль вектора
, a модуль вектора
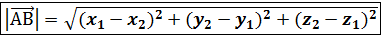
Обозначим углы наклона вектора 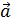 c осями координат ox,oy,oz соответственно
c осями координат ox,oy,oz соответственно 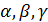 .
.
Определение. Косинусы углов, образованных между вектором и осями координат , называются направляющими косинусами вектора 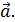
z 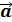 Если вектор
Если вектор 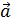 ={ x,y,z} , то x =
={ x,y,z} , то x = 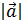
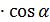 ;
;
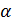
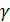
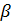 y=
y= 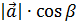 ; z =
; z = 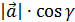 , как проекции ,отсюда
, как проекции ,отсюда
x o y 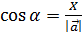 ,
, 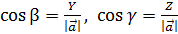 или
или
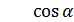 =
= 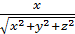 ;
; 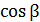 =
= 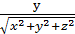 ;
; 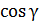 =
= 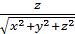 (1)
(1)
Возведём в квадрат обе части равенств (1) и сложим , получим
co 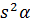 + co
+ co 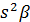 +co
+co 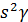 =
= 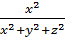 +
+ 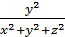 +
+ 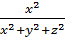 = 1.
= 1.
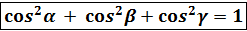
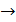 условие того , что
условие того , что 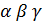 углы вектора с осями координат.
углы вектора с осями координат.
Условия коллинеарности двух векторов
Пусть вектор 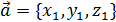 коллинеарен вектору
коллинеарен вектору 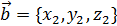 , тогда
, тогда  по теореме (
по теореме ( 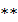 ) имеем
) имеем 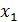 =
= 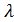
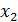 ,
, 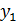 =
= 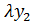 ,
, 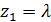
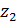 из этих равенств находим
из этих равенств находим 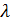 , то есть
, то есть 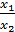
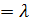 ;
; 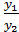
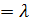 ;
;  =
= 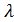 , приравниваем левые части этих равенств
, приравниваем левые части этих равенств 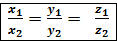
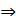 условие коллинеарности векторов.
условие коллинеарности векторов.
Правило.Если векторы коллинеарны , то их координаты пропорциональны.
Определение. Единичный вектор , направленный по вектору 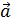 , называется его ортом и обозначается
, называется его ортом и обозначается 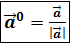
Пример. Найти орт вектора 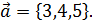
Решение.Найдём модуль вектора 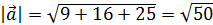 , тогда орт вектора запишется
, тогда орт вектора запишется 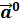 = {
= { 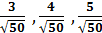 } .
} .
Дата добавления: 2016-06-05; просмотров: 3577;











