Декартова система координат ( д.с.к.)
Определение. Аффинный базис { O, 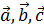 } , у которого векторы
} , у которого векторы 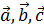 лежат на взаимно ортогональных осях и длины равны единицы, называется декартовым ортогональным базисом , принято обозначать { 0,
лежат на взаимно ортогональных осях и длины равны единицы, называется декартовым ортогональным базисом , принято обозначать { 0, 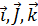 }.
}.
В силу теоремы о разложении вектора в базисе для д.с.к. 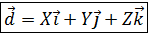
X,Y,Z – координаты вектора , 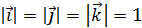 – орты .
– орты .
Теорема. Декартовы прямоугольные координаты X,Y,Z вектора 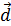 равны ортогональным проекциям этого вектора на оси OX, OY, OZ соответственно.
равны ортогональным проекциям этого вектора на оси OX, OY, OZ соответственно.
Доказательство. Сделаем рисунок
Z 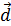
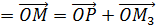
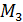
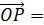
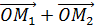
M 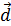 =
= 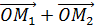 +
+ 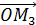
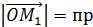 xOM ;
xOM ;
k 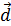
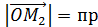 y OM;
y OM;
o j 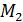 y
y 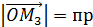 z OM;
z OM;
i по построению.
 P
P
x 24
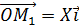 ;
; 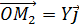 ;
; 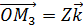 , так как коллинеарны.
, так как коллинеарны.
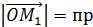 xOM =
xOM = 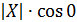 °
° 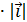 =
= 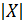 ;
; 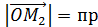 y OM=
y OM= 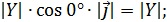
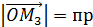 z OM =
z OM = 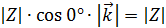 ч. т. д.
ч. т. д.
Определение.Проекции вектора 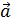 на оси координат называются декартовыми прямоугольнымикоординатами вектора.
на оси координат называются декартовыми прямоугольнымикоординатами вектора.
Теорема  Линейные операции над векторами сводятся к точно таким же линейным операциям над их одноимёнными координатами.
Линейные операции над векторами сводятся к точно таким же линейным операциям над их одноимёнными координатами.
Пример.Найти координаты вектора 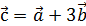 , если
, если 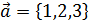 ;
; 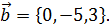
Решение. По теореме 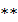 xc=1+3
xc=1+3 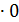 =1; yc =2+3
=1; yc =2+3 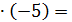 -13; zc = 3+3
-13; zc = 3+3  3= 12
3= 12
Ответ.  = {1, -13, 12}.
= {1, -13, 12}.

Определение. Радиус вектор – это вектор , соединяющий начало координат и точку А , обозначается 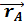 = { X,Y,Z}.
= { X,Y,Z}.
Дата добавления: 2016-06-05; просмотров: 2073;











