Деление отрезка в данном отношении
Определение.Разделить отрезок 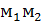 в данном отношении
в данном отношении 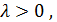 это значит найти на данном отрезке такую точку М , что имеет место равенство
это значит найти на данном отрезке такую точку М , что имеет место равенство 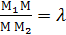 или М1М
или М1М 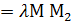 .
.
Пусть даны точки 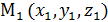 и
и 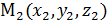 , найдём координаты точки М (x , y, z ) , делящей отрезок
, найдём координаты точки М (x , y, z ) , делящей отрезок 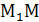 2 в отношении
2 в отношении 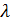 .
.
Z М1 М 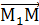 = { x - x1 , y – y1 , z – z1 } ;
= { x - x1 , y – y1 , z – z1 } ;
M2 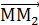 = { x2 – x , y2 – y , z2 – z }.
= { x2 – x , y2 – y , z2 – z }.
x o y 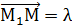
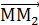 по теореме (
по теореме (  ) в координатах
) в координатах
x – x1 = 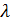 (x2 – x)
(x2 – x)  x (1+
x (1+ 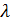 )=
)= 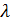 x2 +x1
x2 +x1 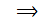 x =
x = 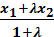 y – y1 =
y – y1 = 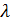 ( y2 – y )
( y2 – y )  y (1+
y (1+ 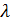 ) =
) = 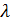 y2 + y1
y2 + y1  y =
y = 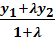
z – z1 = 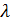 ( z2 – z )
( z2 – z )  z (1+
z (1+ 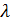 ) =
) = 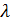 z2 + z1
z2 + z1  z =
z = 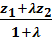
Если точка М середина отрезка , то М1 М = М М2 и 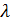 = 1 , тогда
= 1 , тогда
Xcp. = 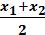 , Ycp. =
, Ycp. = 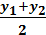 , Zcp. =
, Zcp. = 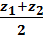 .
.
Если 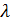 < 0 , то точка М лежит вне отрезка М1 М2 .
< 0 , то точка М лежит вне отрезка М1 М2 .
ЛЕКЦИЯ 7. Скалярное произведение векторов. Векторное произведение.
Определение.Скалярным произведением векторов 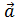 и
и 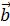 называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними.
Обозначается ( 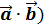 =
= 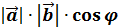
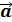

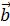
Физический смысл скалярного произведения
Из физики известно , что работа силы по перемещению , находится по формуле А = F  S
S 
 F
F
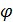
S
Если 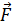 вектор силы , а
вектор силы , а  вектор перемещения , то работа А =
вектор перемещения , то работа А = 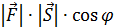 = = (
= = ( 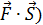 , то есть работа равна скалярному произведению векторов силы и пути
, то есть работа равна скалярному произведению векторов силы и пути
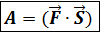
Свойства скалярного произведения
1. ( 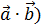
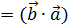 следует из определения;
следует из определения;
2. 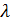 (
( 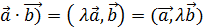 ;
;
3. ( 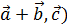 = (
= ( 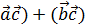 ;
;
4.Если 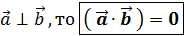 , так как
, так как 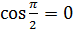 ;
;
5. ( 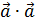
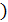
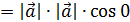 0
0  (
( 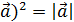 2 или
2 или 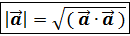
6. ( 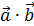
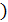 =
= 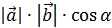
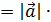
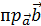

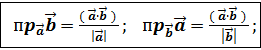
7. ( 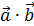 ) =
) = 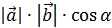

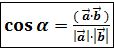
Выражение скалярного произведения
Дата добавления: 2016-06-05; просмотров: 2475;











