ЛЕКЦИЯ 5. Понятие вектора. Основные операции над векторами.

Определение.Пространство , в котором введены декартовы координаты x,y,z, так , что выполняются следующие условия :

1) разным точкам пространства соответствуют разные наборы координат ;

2) каждому набору x,y,z соответствует какая – то точка Р , изучаемого пространства ;

называется 3-х мерным декартовым и обозначается 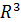; 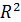– двумерное декартово пространство – плоскость ; 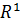- одномерное декартово пространство – прямая. Координаты – (от латинского слова ) упорядоченный , определённый.

Определение. Геометрическим вектором или просто вектором называется направленный отрезок прямой.

Обозначается 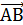, А – начало , В – конец вектора или 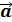или .

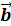Определение. Векторомназывается матрица размерности (n 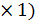или (1 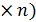; 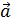= (n ,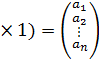

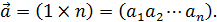
Длинавектора– это его модуль, абсолютная величина,обозначается , .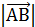

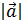Определение.Вектор называется нулевым, если его начало и конец совпадают.

Определение.Векторы называются коллинеарными , если они лежат на одной либо на параллельных прямых , их можно всегда представить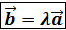

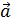
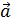
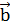
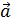
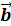
Определение.Векторы называются компланарными , если они лежат в одной

плоскости .

Определение.Два вектора называются равными, если

1) коллинеарны ,

2) имеют одинаковое направление ,

3) имеют равные длины.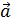

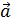
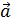
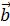
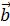
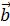
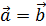
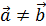
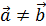Векторы , изучаемые в геометрии, называются свободными , так как точку приложения выбираем произвольно. Есть ещё скользящие и связные в физике и механике. Скользящие – такие, которые считаются равными , если лежат на одной прямой ( сила ). Связные – если, имеют общее начало и равны.